The Philosophy and Physics of Duality (2508.01616v1)

Abstract: This monograph discusses dualities in physics: what dualities are, their main examples--from quantum mechanics and electrodynamics to statistical mechanics, quantum field theory and string theory--and the philosophical questions they raise. Part I first conceptualises dualities and discusses their main roles and themes, including how they are related to familiar notions like symmetry and interpretation. It also discusses the main simple examples of dualities: position-momentum, wave-particle, electric-magnetic, and Kramers-Wannier dualities. Part II discusses advanced examples and their inter-relations: particle-soliton dualities, electric-magnetic dualities in quantum field theories, dualities in string theory, and gauge-gravity duality. This Part ends with discussions of the hole argument, and how string theory counts the microstates of a black hole. Part III is an in-depth discussion of general philosophical issues on which dualities bear: theoretical equivalence (two theories 'saying the same thing, in different words'), scientific realism and the under-determination of theories by data, theory succession and the M-theory programme, explanation, and scientific understanding. It proposes a view of scientific theories that it dubs 'the geometric view of theories'. The book's treatment of the examples is at the advanced undergraduate and graduate level, starting from elementary and progressing to more advanced examples. The discussions of philosophical topics, such as referential semantics, theoretical equivalence, scientific realism and scientific understanding, are both self-contained and in-depth. Thus the book is aimed at students and researchers with an interest in the physical examples and philosophical questions about dualities, and also in how physics and philosophy can fruitfully interact with each other.

• The paper provides a formal schema for duality, showing that isomorphic mappings between models preserve the values of physical quantities.
• It distinguishes between bare theories and model-specific structures, clarifying conditions for internal versus external interpretations and physical equivalence.
• The analysis links abstract symmetry with practical applications, offering insights into quantum mechanics, gauge theory, and string theory.

The Philosophy and Physics of Duality: A Technical Analysis

Introduction and Motivation

"The Philosophy and Physics of Duality" (2508.01616) provides a comprehensive, formal account of duality in physics, integrating both technical and philosophical perspectives. The authors develop a precise schema for duality, grounded in the mathematical structure of physical theories, and systematically analyze its implications for theoretical equivalence, interpretation, and the methodology of physics. The work is situated at the intersection of mathematical physics, philosophy of science, and the foundations of quantum field theory and string theory.

Formal Schema for Duality

The central thesis is that a duality is an isomorphism between two models (in the sense of mathematical representations) of a common core theory, typically formalized as a triple $$\langle \mathcal{S}, \mathcal{Q}, \mathcal{D} \rangle$$ of state space, quantities, and dynamics. The duality is realized by a pair of bijections $$d_{\mathcal{S}}: \mathcal{S}_{M_1} \to \mathcal{S}_{M_2}$$ and $$d_{\mathcal{Q}}: \mathcal{Q}_{M_1} \to \mathcal{Q}_{M_2}$$, such that the values of physical quantities are preserved:

$$\forall s_1 \in \mathcal{S}_{M_1}, \forall Q_1 \in \mathcal{Q}_{M_1},\quad \langle Q_1, s_1 \rangle_1 = \langle d_{\mathcal{Q}}(Q_1), d_{\mathcal{S}}(s_1) \rangle_2$$

and the dynamics is equivariant under the duality maps.

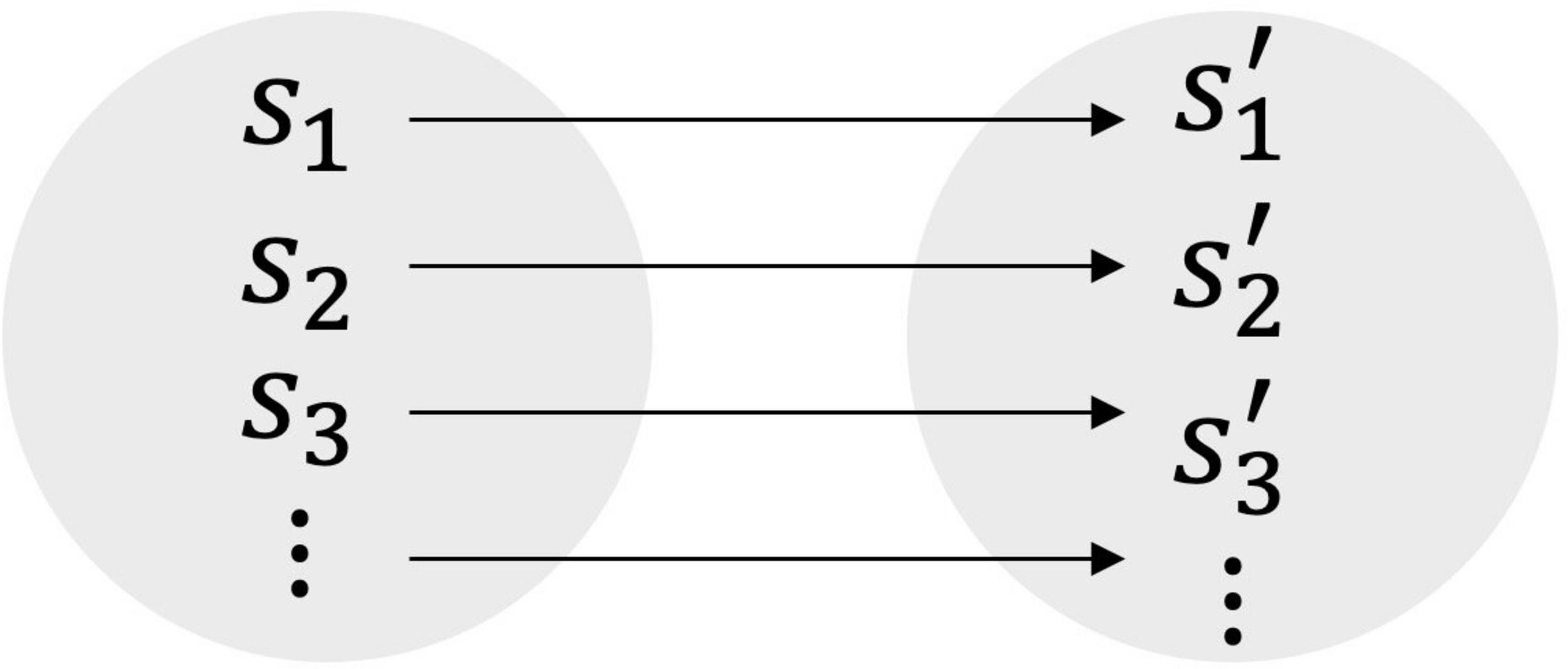
Figure 1: On the left, a theory with the set of states $s_1, s_2, s_3, \ldots$ and, on the right, a theory with the set of states $s'_1, s'_2, s'_3, \ldots$. The duality maps the states of one theory to the states of the other theory, such that the values of their respective quantities match.

This formalism is sufficiently general to encompass both classical and quantum dualities, including position-momentum duality in quantum mechanics, electric-magnetic duality in gauge theory, and Kramers-Wannier duality in statistical mechanics.

The Common Core Theory and Model Structure

A key innovation is the explicit distinction between the bare theory (the common core) and its models (representations with additional specific structure). The bare theory is typically an abstract mathematical structure, while each model is a concrete realization, possibly with extra structure not present in the core. Duality is then an isomorphism at the level of the model roots, not necessarily extending to the specific structure.

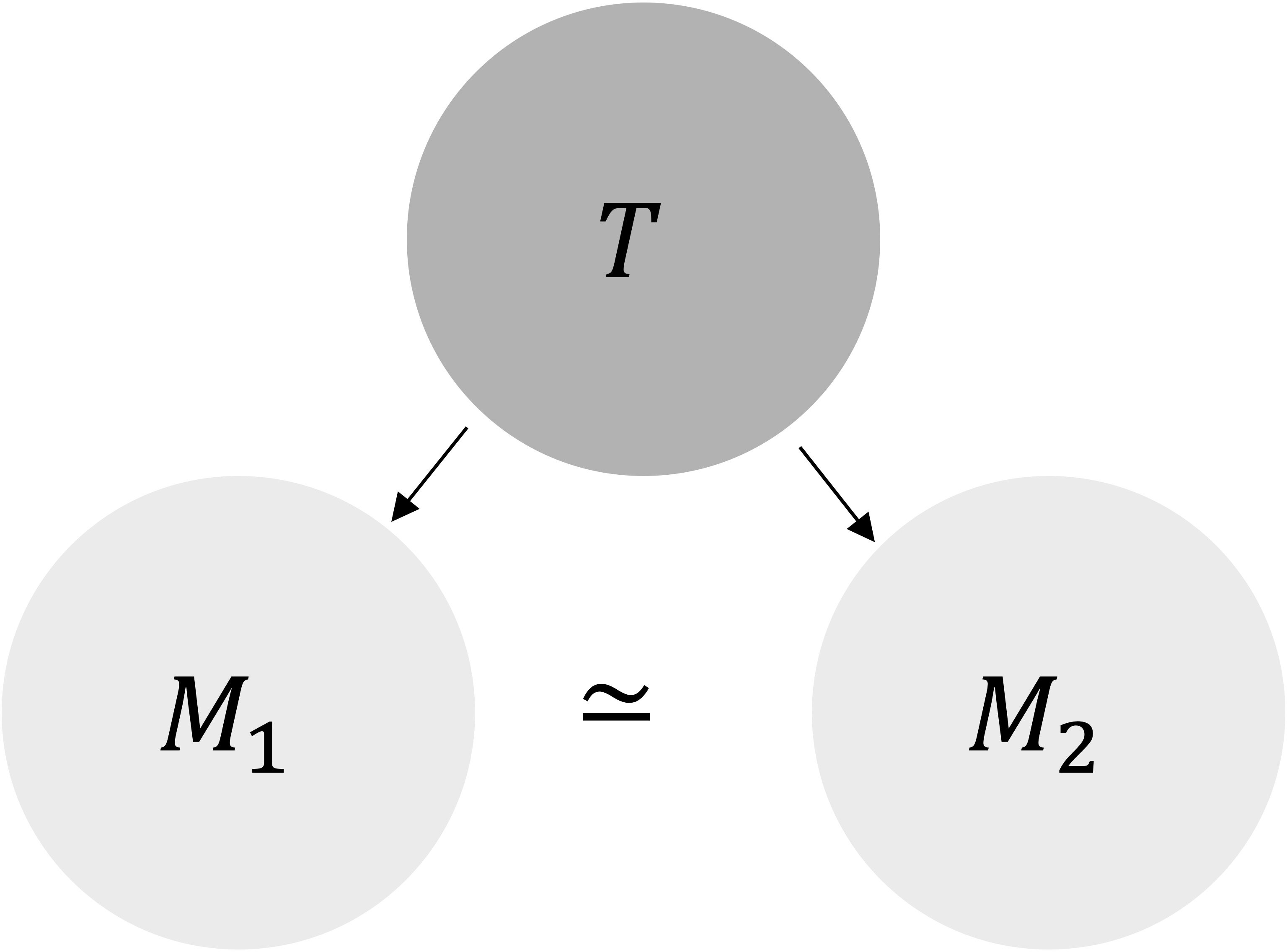
Figure 2: A common core theory, $T$, with two dual (i.e.~isomorphic) representations, $M_1$ and $M_2$.

This layered approach allows for a rigorous analysis of when two models are genuinely dual (isomorphic as representations of the core) versus when they are merely analogous or related by a weaker correspondence (quasi-duality).

Interpretation, Internal/External Semantics, and Theoretical Equivalence

The authors adopt a referential semantics for physical theories, distinguishing between internal interpretations (mapping only the model root) and external interpretations (mapping also the specific structure). This distinction is crucial for analyzing when dual models are physically equivalent (i.e., make the same claims about the world) versus when they are merely formally isomorphic but physically inequivalent.

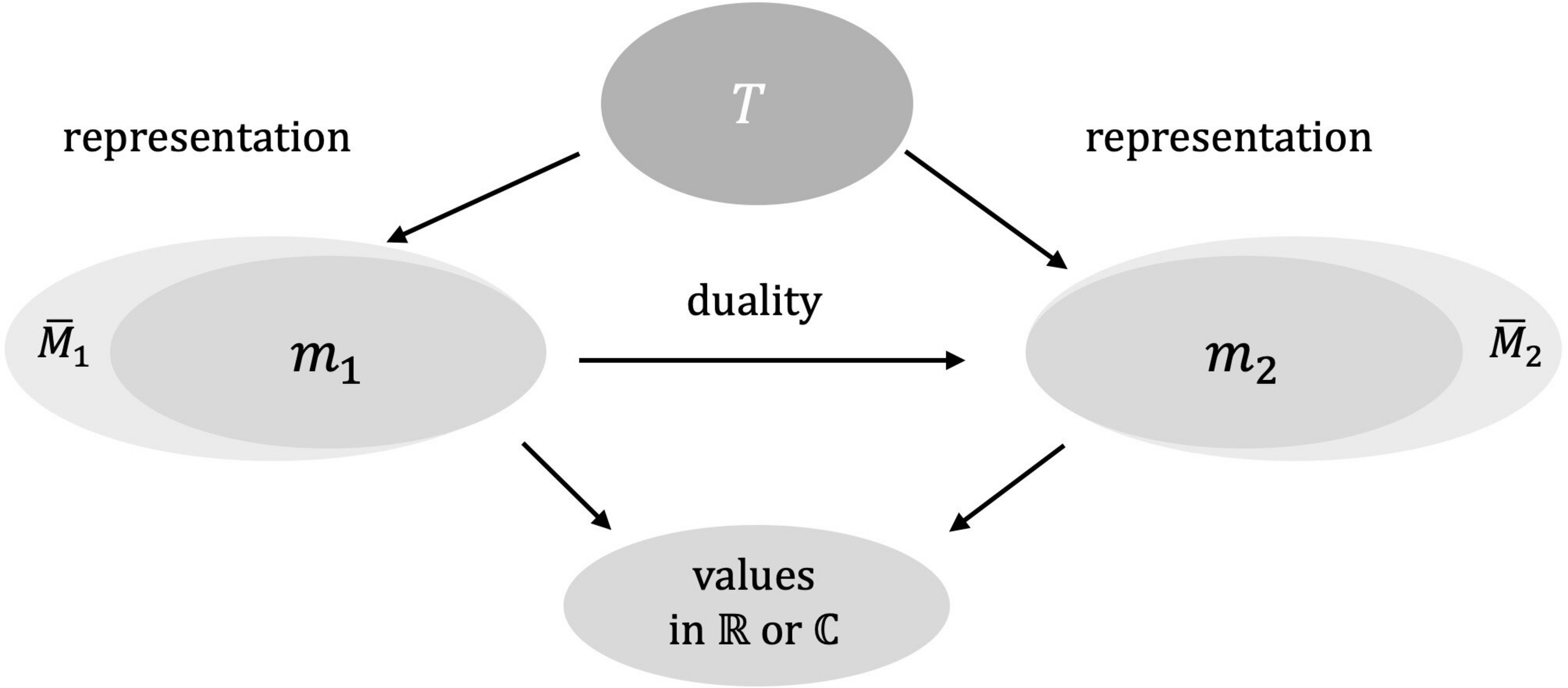
Figure 3: Relation between the bare theory "above" and its two duals, as representations, "below". The duality maps one model into the other. The isomorphism preserves the values of quantities.

A sufficient condition for physical equivalence is the existence of internal interpretations forming a commuting triangle with the duality map, ensuring that both models are interpreted as describing the same sector of reality. External interpretations, by contrast, may break this equivalence if the specific structure is mapped differently.

Symmetry, Duality, and Hierarchies

The schema situates duality as a "giant symmetry"—an isomorphism not just of states within a single model, but between entire models of a theory. The analysis distinguishes:

• Stipulated symmetries: symmetries required by the definition of the bare theory, which all models must represent.
• Accidental symmetries: symmetries present in the bare theory but not required in all models.
• Proper symmetries of models: symmetries of the specific structure, not shared by all models or the core.

This hierarchy clarifies the relationship between duality and gauge symmetry, and explains why duality is not, in general, a gauge redundancy.

Exemplars and Applications

The schema is illustrated with canonical examples:

• Position-momentum duality: The Fourier transform provides a unitary equivalence between the position and momentum representations of quantum mechanics, preserving all expectation values and dynamics.
• Electric-magnetic duality: Maps electric charges to magnetic charges, often relating weak and strong coupling regimes.
• Kramers-Wannier duality: Relates high- and low-temperature regimes of the Ising model, but does not entail physical equivalence due to differing temperature standards.

  Figure 4: Position and momentum operators, and their representations. Top row: representation-independent operators, ${\bf\hat X}$ and ${\bf\hat P}$.

The analysis extends to advanced dualities in quantum field theory and string theory, including gauge-gravity duality, where the dual models may differ in spacetime dimension, field content, and interpretation, yet are isomorphic as representations of a common core.

Philosophical Implications: Theoretical Equivalence, Realism, and Under-determination

The work provides a rigorous framework for addressing debates on theoretical equivalence and under-determination. Duality, as formal isomorphism, does not automatically entail physical equivalence; this depends on the interpretative stance (internal vs. external). The schema thus clarifies when dualities pose a challenge to scientific realism and when they do not.

The authors also analyze the role of dualities in theory construction, unification, and the emergence of new physics, emphasizing the heuristic and practical functions of dualities beyond their formal role.

Methodological and Structural Insights

A significant contribution is the geometric view of theories: the idea that the space of models (or "theory space") may have a nontrivial structure, with dualities relating different "patches" or regimes. This perspective is particularly salient in string theory, where dualities suggest the existence of a deeper, possibly non-perturbative, theory (e.g., M-theory) of which known models are local approximations.

Figure 5: Plan of the book and its three Parts. The arrows on the left propose a reading sequence for philosophy readers, and on the right for physics readers. We expect philosophy of physics readers to be in a superposition of two "timelines".

Future Directions and Open Problems

The schema provides a robust platform for further research on:

• The formal classification of dualities and quasi-dualities in quantum field theory and string theory.
• The development of more general mathematical frameworks (e.g., category theory, higher structures) for representing dualities.
• The analysis of dualities in the context of emergent spacetime, holography, and the foundations of quantum gravity.
• The epistemic and pragmatic roles of dualities in theory development, explanation, and scientific understanding.

Conclusion

This work offers a technically precise, conceptually rich account of duality, integrating mathematical rigor with philosophical analysis. By formalizing duality as isomorphism of models with respect to a common core, and by distinguishing internal and external interpretations, the authors provide a powerful framework for analyzing theoretical equivalence, the structure of physical theories, and the methodological significance of dualities in contemporary physics. The schema is applicable across a wide range of physical contexts and sets a new standard for the systematic paper of duality in both physics and philosophy.