Co-Reward: Self-supervised Reinforcement Learning for Large Language Model Reasoning via Contrastive Agreement (2508.00410v1)

Abstract: Although reinforcement learning with verifiable rewards (RLVR) shows promise in improving the reasoning ability of LLMs, the scaling up dilemma remains due to the reliance on human annotated labels especially for complex tasks. Recent alternatives that explore various self-reward signals exhibit the eliciting potential of LLM reasoning, but suffer from the non-negligible collapse issue. Inspired by the success of self-supervised learning, we propose \textit{Co-Reward}, a novel RL framework that leverages contrastive agreement across semantically analogical questions as a reward basis. Specifically, we construct a similar question for each training sample (without labels) and synthesize their individual surrogate labels through a simple rollout voting, and then the reward is constructed by cross-referring the labels of each question pair to enforce the internal reasoning consistency across analogical inputs. Intuitively, such a self-supervised reward-shaping mechanism increases the difficulty of learning collapse into a trivial solution, and promotes stable reasoning elicitation and improvement through expanding the input sample variants. Empirically, Co-Reward achieves superior performance compared to other self-reward baselines on multiple reasoning benchmarks and LLM series, and reaches or even surpasses ground-truth (GT) labeled reward, with improvements of up to $+6.8\%$ on MATH500 over GT reward on Llama-3.2-3B-Instruct. Our code is publicly available at https://github.com/tmlr-group/Co-Reward.

• The paper introduces Co-Reward, which leverages contrastive agreement via semantically analogous questions to shape self-supervised rewards.
• The approach mitigates training collapse and ensures stable reasoning in LLMs, outperforming other self-reward baselines by up to +6.8%.
• The method employs majority voting and pseudo-labeling to enhance reasoning robustness across benchmarks and multiple language models.

Co-Reward: Contrastive Agreement for LLM Reasoning

This paper introduces Co-Reward, a novel self-supervised RL framework designed to enhance the reasoning capabilities of LLMs. The core idea revolves around using contrastive agreement across semantically analogous questions as a basis for reward shaping. By constructing similar questions for each training sample and synthesizing surrogate labels via rollout voting, the framework constructs rewards that enforce internal reasoning consistency. This approach mitigates the training collapse issue often encountered in self-reward methods and promotes stable reasoning elicitation.

Contrastive Agreement Framework

Co-Reward leverages a contrastive agreement principle inspired by self-supervised learning. The framework aims to capture intrinsic representation by using input-level variants to refine reasoning. Given an input, the method generates rephrased prompts with equivalent semantic intent. The model's responses to these analogs are aggregated by majority voting to form a pseudo-consensus answer, which is then used to supervise the original input through a reward signal. The authors illustrate the Co-Reward framework in (Figure 1).

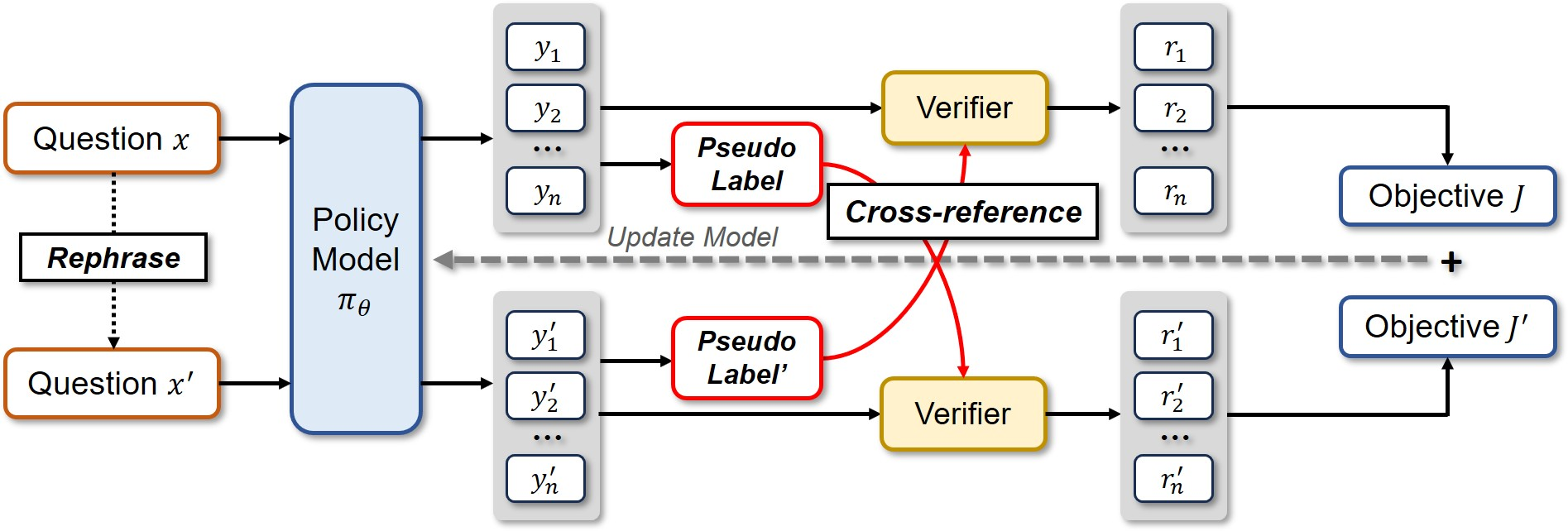
Figure 1: Illustration of Co-Reward Framework: given the original questions in training set, we generate the paraphrased version for model to response, then we use the majority-voted answers of each as pseudo-labels to cross-overly supervise the model learning on original and new questions.

This dual-path structure shapes the reward by using each majority-voted answer as a cross-reference to the paired questions for optimization. This explicitly expands the input coverage for reasoning validity. The method encourages the model to reinforce reasoning strategies robust to linguistic variation, while suppressing trivial solutions.

Algorithmic Implementation

The Co-Reward framework is algorithmically realized through a modified GRPO objective. The objective function, expressed in Equation 1, includes terms for both original and rephrased questions:

$\mathcal{J}_\textrm{Co-Reward}(\theta) \; = \;{\mathbb{E}_{{x\sim D},\{{y_i}\}_{i=1}^G\sim \pi_{\theta_\textrm{old}({Y|x})}\mathcal{R}(\hat{A})}}_{\mathcal{J}_\textrm{{\textcolor{blue}{original}(\theta)}\;+\; {\mathbb{E}_{{x'\sim D'},\{{y_i}'}\}_{i=1}^G\sim \pi_{\theta_\textrm{old}({Y'|x'})}\mathcal{R}(\hat{A}')}_{\mathcal{J}_\textrm{{\textcolor{brown}{rephrased}(\theta)}}$

The relative advantages, as shown in Equation 2, are estimated using cross-referenced supervision, where the voted answer of the rephrased question supervises the original question and vice versa:

$\hat{A}_{i} = \frac{r_i({y'_\textrm{v},{y_i}) - \text{mean}(\{r_i({y'_\textrm{v},{y_i})\}_{i=1}^{G})}{\text{std}(\{r_i({y'_\textrm{v},{y_i})\}_{i=1}^{G})},\; \hat{A}'_{i} = \frac{r_i({y_\textrm{v},{y_i'}) - \text{mean}(\{r_i({y_\textrm{v},{y_i'})\}_{i=1}^{G})}{\text{std}(\{r_i({y_\textrm{v},{y_i'})\}_{i=1}^{G})}$

The majority voting mechanism, detailed in Equation 3, is used to generate pseudo-labels for both original and rephrased questions:

${y_\textrm{v}\leftarrow{\arg\max_{y*}\sum_{i=1}^n \mathrm{1}[\textrm{ans}({y_i})=\textrm{ans}(y*)]},\quad {y_\textrm{v}'}\leftarrow{\arg\max_{y*}\sum_{i=1}^n \mathrm{1}[\textrm{ans}({y_i'})=\textrm{ans}(y*)]}$

Experimental Results

The authors evaluated Co-Reward on a series of reasoning benchmarks using models such as the Llama and Qwen series. The results indicate that Co-Reward outperforms other self-reward baselines across multiple reasoning benchmarks and LLM series. For example, Co-Reward achieves improvements of up to $+6.8\%$ over GT reward on Llama-3.2-3B-Instruct. Additionally, the method demonstrates superior test-time training performance due to its independence from ground-truth labels. The validation curves on MATH5000, depicted in (Figure 2), illustrate the stability of Co-Reward compared to baselines.

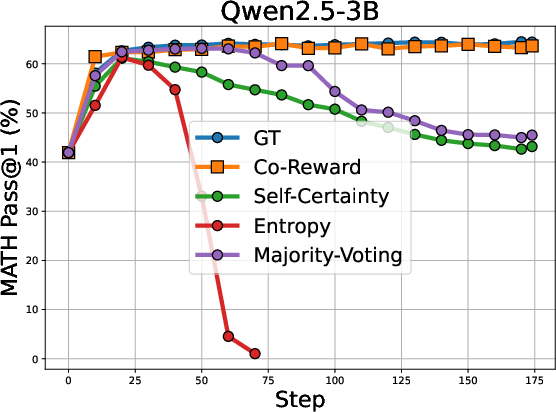
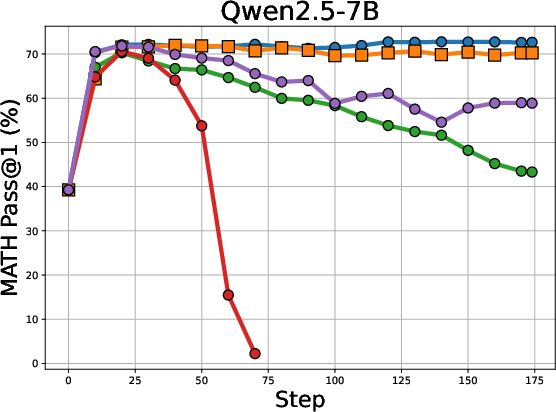
Figure 2: Validation curves on MATH5000 of Co-Reward with baselines. We can find the learning of Co-Reward is generally stable without significant performance drop across different LLMs.

Further analysis of voting accuracy during training shows that Co-Reward produces more stable and robust voted answers and mitigates the collapse of the voting strategy on challenging problems.

Analysis of Voting Accuracy

The voting accuracy across different LLMs during training is illustrated in (Figure 3).

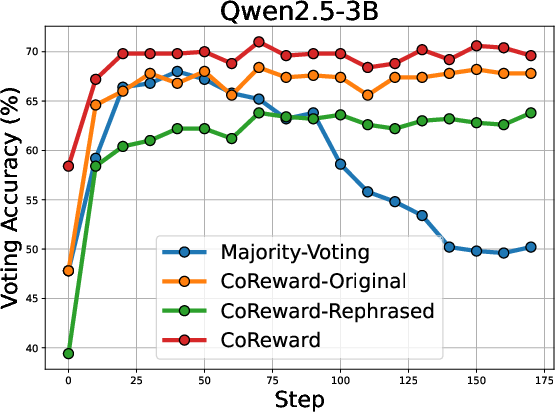
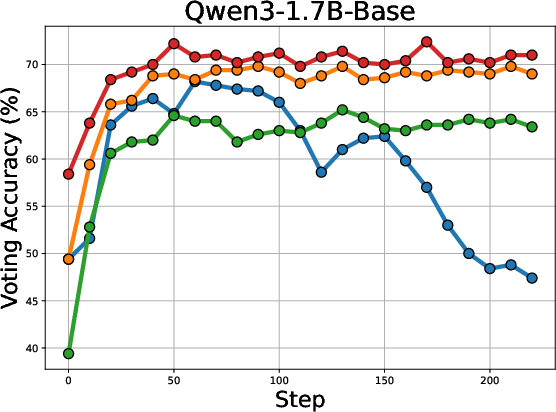
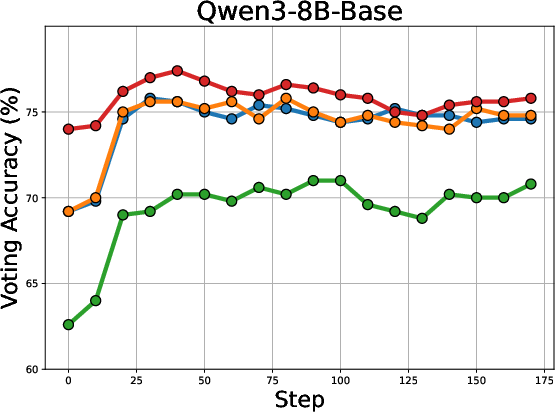
Figure 3: Voting accuracy (\%) across different LLMs with increasing training steps.

The figure shows that Co-Reward maintains stable voting accuracy compared to the Majority-Voting baseline, attributed to the cross-reference pseudo-labeling strategy.

The voting accuracy for different difficulty levels of math problems is shown in (Figure 4).

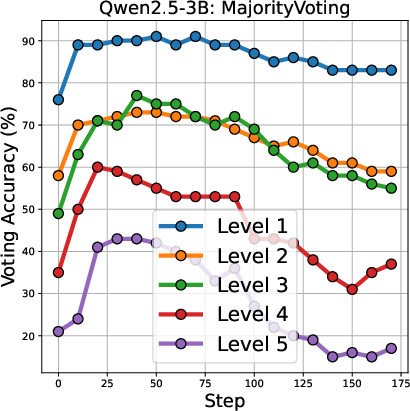
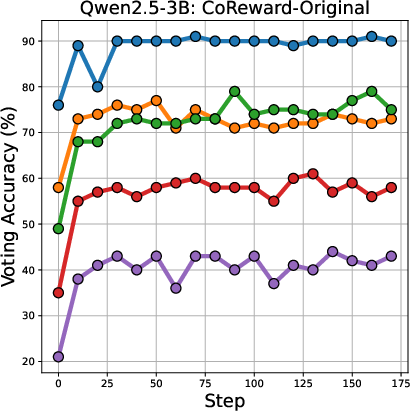
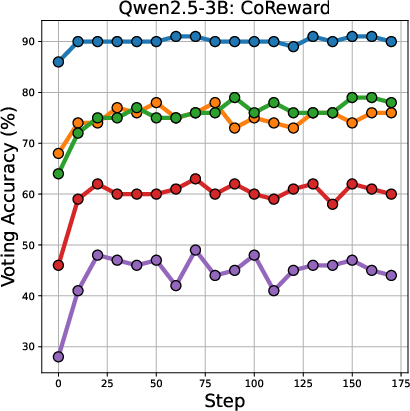
Figure 4: Voting accuracy across different difficulty level of math problems.

The results indicate that Majority-Voting suffers a drop in accuracy on more difficult problems, while Co-Reward maintains stable accuracy across all difficulty levels.

Qualitative Analysis

A case paper, presented in (Figure 5), compares the generated content for the same math problem across Co-Reward, Majority-Voting, Self-Certainty, and Entropy.

Figure 5: Case paper of the Qwen3-1.7B-Base generation trained by four self-supervised methods.

The analysis reveals that Co-Reward produces a well-structured reasoning process and arrives at the correct answer, while Majority-Voting exhibits reward hacking, and Self-Certainty and Entropy suffer from repetition problems.

Conclusion

This work presents Co-Reward, a self-supervised RL framework that elicits latent reasoning capabilities of LLMs through contrastive agreement. By leveraging analogy across semantically equivalent question rewrites and employing majority voting, Co-Reward constructs robust, cross-referable reward signals without requiring explicit labels. The method promotes stable and genuine reasoning improvements by considering broader input-side coverage. This approach offers a promising direction for future exploration into self-supervised RL for reasoning to advance the development of LLM-based reasoning systems.