Embryology of a Language Model (2508.00331v1)

Abstract: Understanding how LLMs develop their internal computational structure is a central problem in the science of deep learning. While susceptibilities, drawn from statistical physics, offer a promising analytical tool, their full potential for visualizing network organization remains untapped. In this work, we introduce an embryological approach, applying UMAP to the susceptibility matrix to visualize the model's structural development over training. Our visualizations reveal the emergence of a clear body plan,'' charting the formation of known features like the induction circuit and discovering previously unknown structures, such as aspacing fin'' dedicated to counting space tokens. This work demonstrates that susceptibility analysis can move beyond validation to uncover novel mechanisms, providing a powerful, holistic lens for studying the developmental principles of complex neural networks.

• The paper introduces susceptibility analysis to visualize the emergence of internal computational structures in language models during training.
• It employs UMAP and PCA to uncover distinctive developmental patterns such as the 'rainbow serpent', induction circuit, and spacing fin.
• The study demonstrates that these structural evolutions are robust across seeds and correlate with generalization error through local learning coefficients.

Embryological Visualization of LLM Development via Susceptibility Analysis

Introduction

The paper "Embryology of a LLM" (2508.00331) presents a novel approach to understanding the developmental dynamics of neural LLMs by leveraging susceptibility analysis and dimensionality reduction. Drawing an analogy to biological embryology, the authors treat the training process as a form of developmental morphogenesis, where the internal computational structure of a randomly initialized transformer emerges and specializes over time. The central technical innovation is the use of per-token susceptibility vectors—quantities from statistical physics that measure the covariance between model components and token prediction loss—projected into low-dimensional space via UMAP to visualize the evolution of model structure.

Susceptibility Vectors and Structural Inference

The susceptibility vector $\eta_w(xy)$ for a token $y$ in context $x$ is defined as the tuple of per-component susceptibilities $(\chi^{C_1}_{xy}, \ldots, \chi^{C_H}_{xy})$, where each $\chi^{C_j}_{xy}$ quantifies the covariance between perturbations in the weights of component $C_j$ and the loss for predicting $y$ given $x$. Negative susceptibility indicates that a component expresses the continuation $y$ (i.e., perturbations that improve $p(y|x)$ also improve overall loss), while positive susceptibility indicates suppression.

By sampling token sequences and computing their susceptibility vectors, the authors construct a high-dimensional point cloud representing the model's internal response landscape. Dimensionality reduction via UMAP yields a visualization of the "data manifold" as perceived by the model, revealing functional specialization and the emergence of computational circuits.

Visualization of Developmental Trajectories

At the end of training, the UMAP projection of susceptibility vectors forms a distinctive structure termed the "rainbow serpent," with token sequences colored by pattern (e.g., word start, word end, induction, spacing, delimiter, formatting, numeric). The principal axes of the UMAP correspond to global expression/suppression (anterior-posterior) and induction circuit specialization (dorsal-ventral).

Figure 1: The rainbow serpent: UMAP projection of susceptibility vectors for a 3M parameter LLM at the end of training, colored by token pattern.

The developmental trajectory is tracked across four critical checkpoints, corresponding to distinct learning stages identified via the local learning coefficient (LLC). Early in training, the UMAP is thin and unstratified; as training progresses, token patterns differentiate and organize along the principal axes, with induction patterns separating from other tokens and spacing tokens forming a distinct "fin" structure.

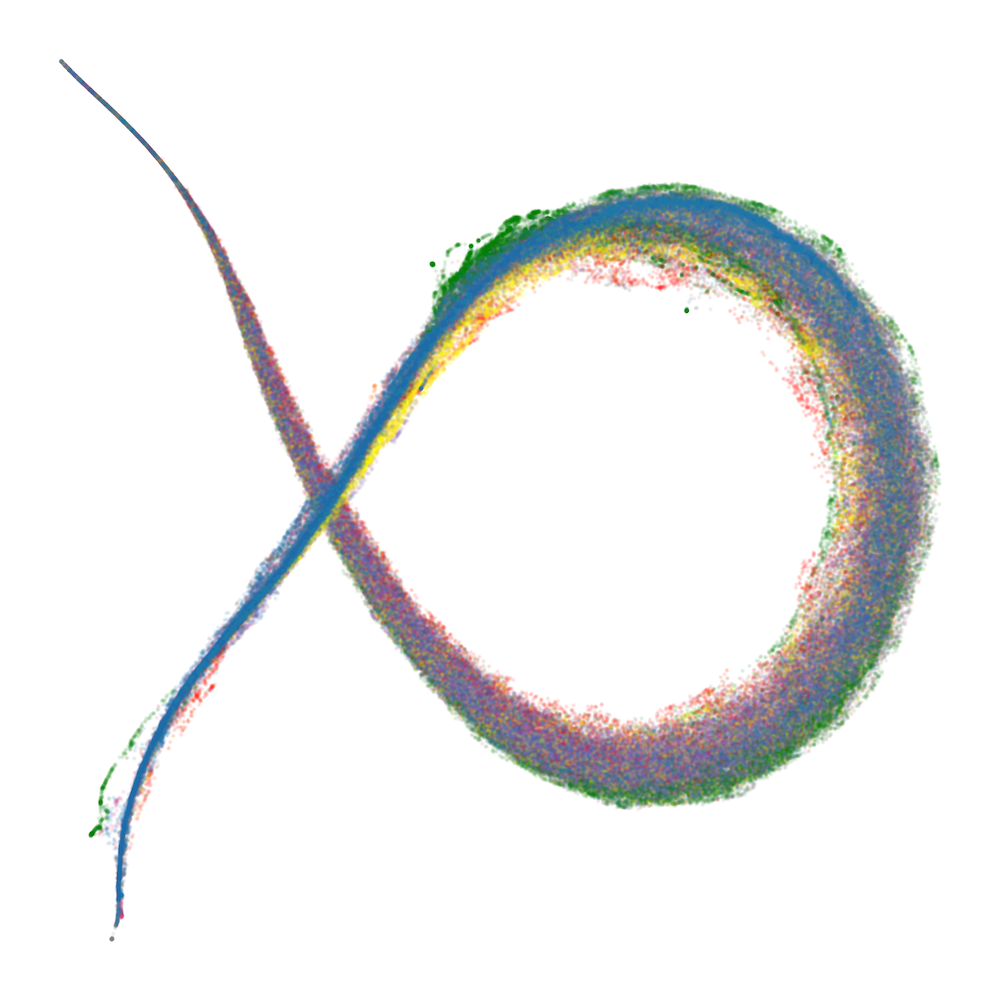
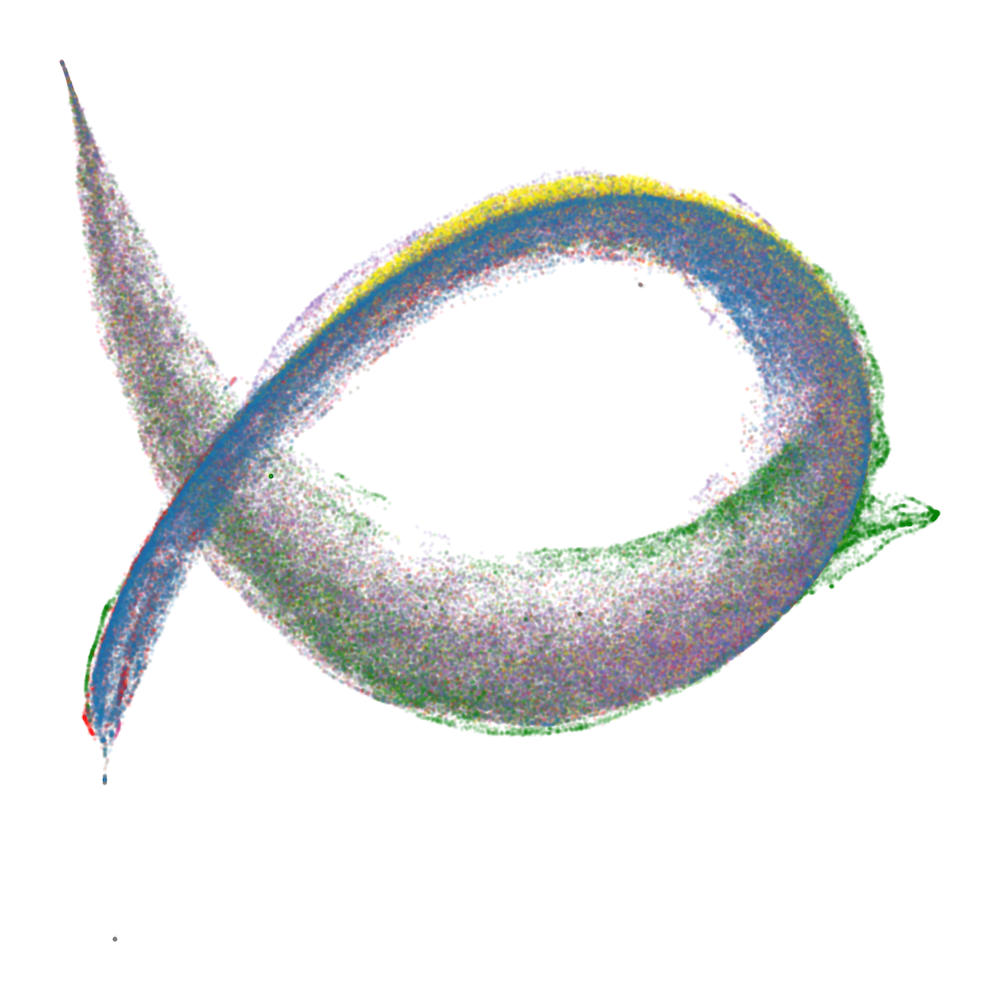
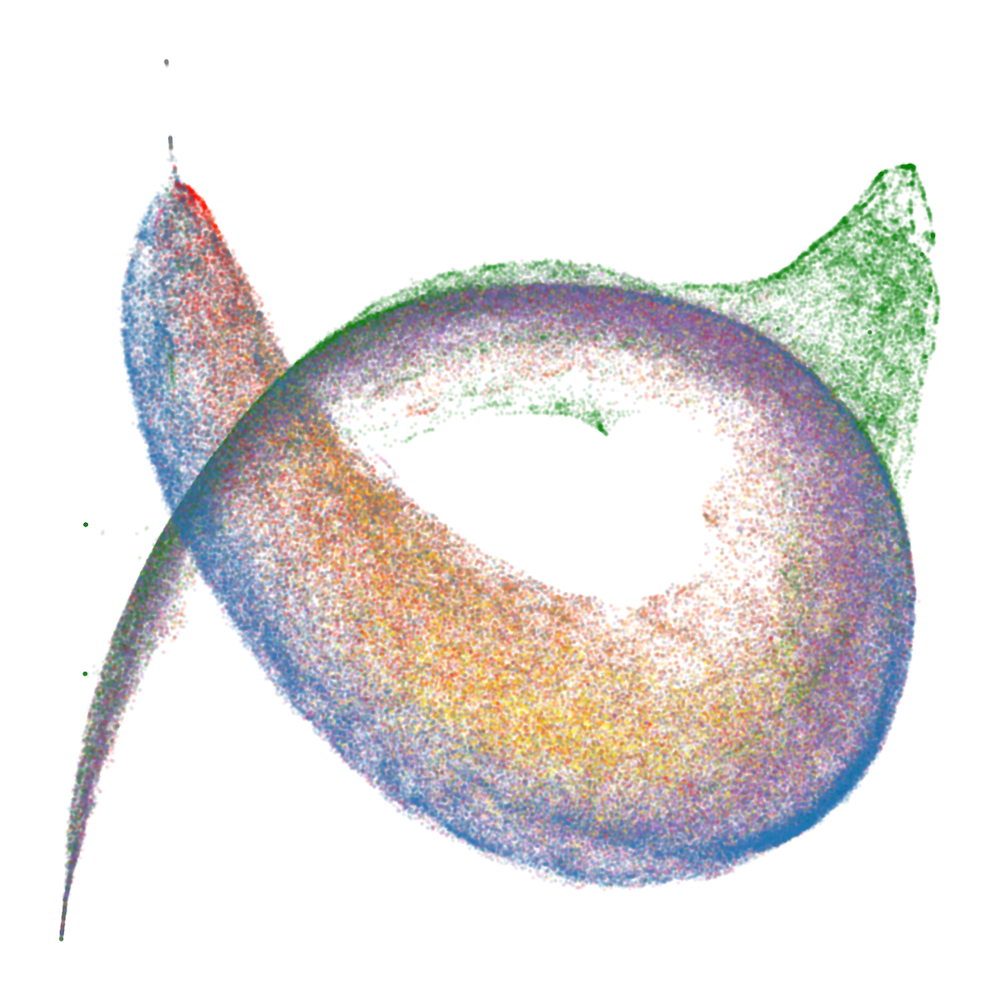
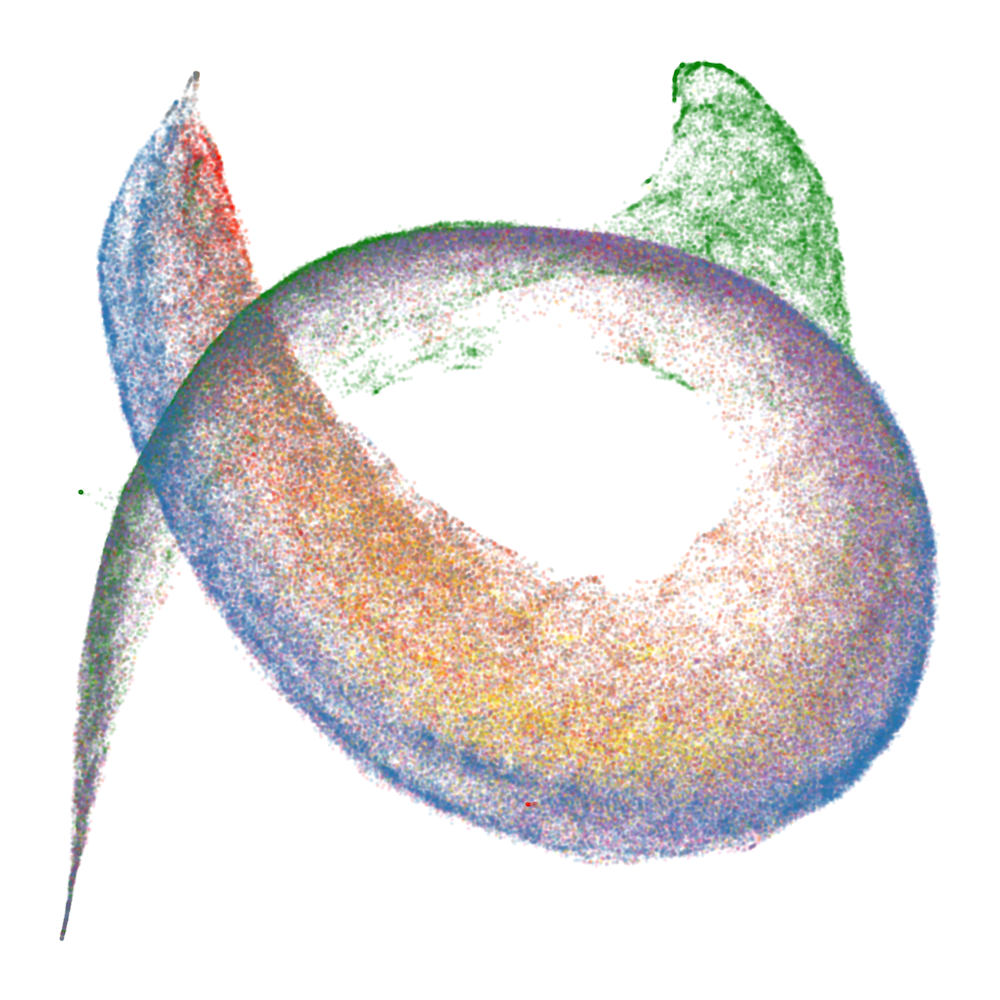
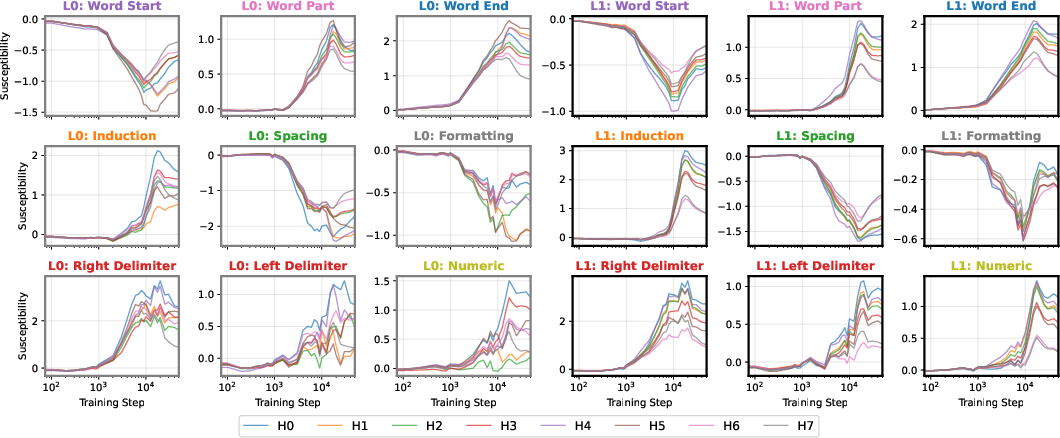
Figure 2: Embryology of the rainbow serpent: UMAP projections of per-token susceptibilities across training, showing stratification by token pattern and thickening along the dorsal-ventral axis.

Emergence of Known and Novel Structures

Induction Circuit Formation

The induction circuit, previously characterized in mechanistic interpretability literature, emerges as a thickening along the dorsal-ventral axis in the UMAP. PCA analysis of susceptibility vectors reveals that the heads involved in induction (e.g., previous-token and induction heads) load strongly on the second principal component, and induction pattern tokens become increasingly separated from other tokens as training progresses.

Figure 3: Per-token susceptibility PCA showing loadings of principal components on data patterns, quantifying the separation of induction patterns.

Spacing Fin: A Novel Computational Structure

A previously unreported structure, the "spacing fin," emerges as a cluster of spacing tokens (spaces, newlines, tabs) that are differentiated by the number of preceding spacing tokens in context. This fin is visible as an extrusion from the main body in the UMAP and is quantitatively characterized by the direction in susceptibility space associated with increasing consecutive spacing tokens.

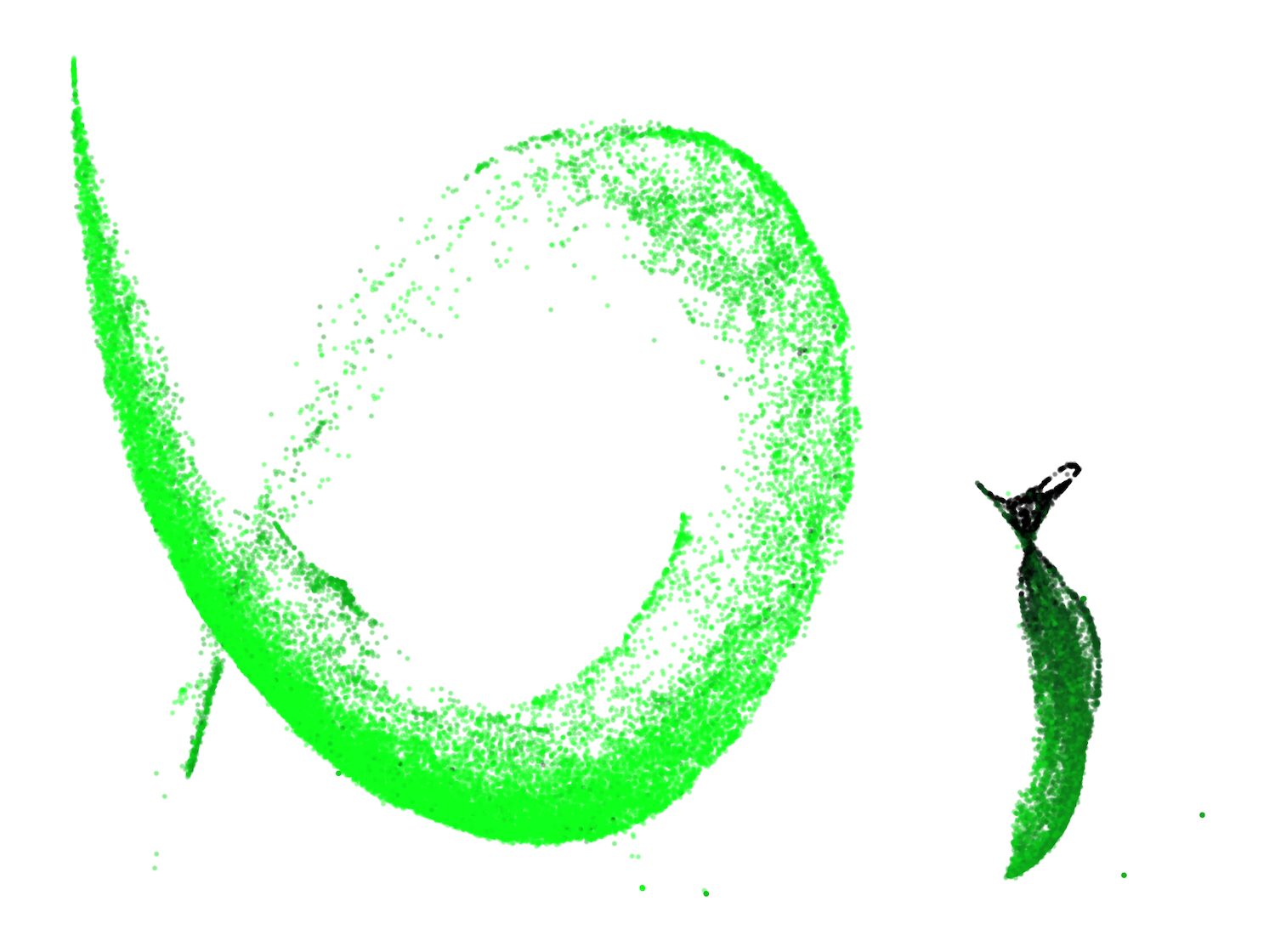
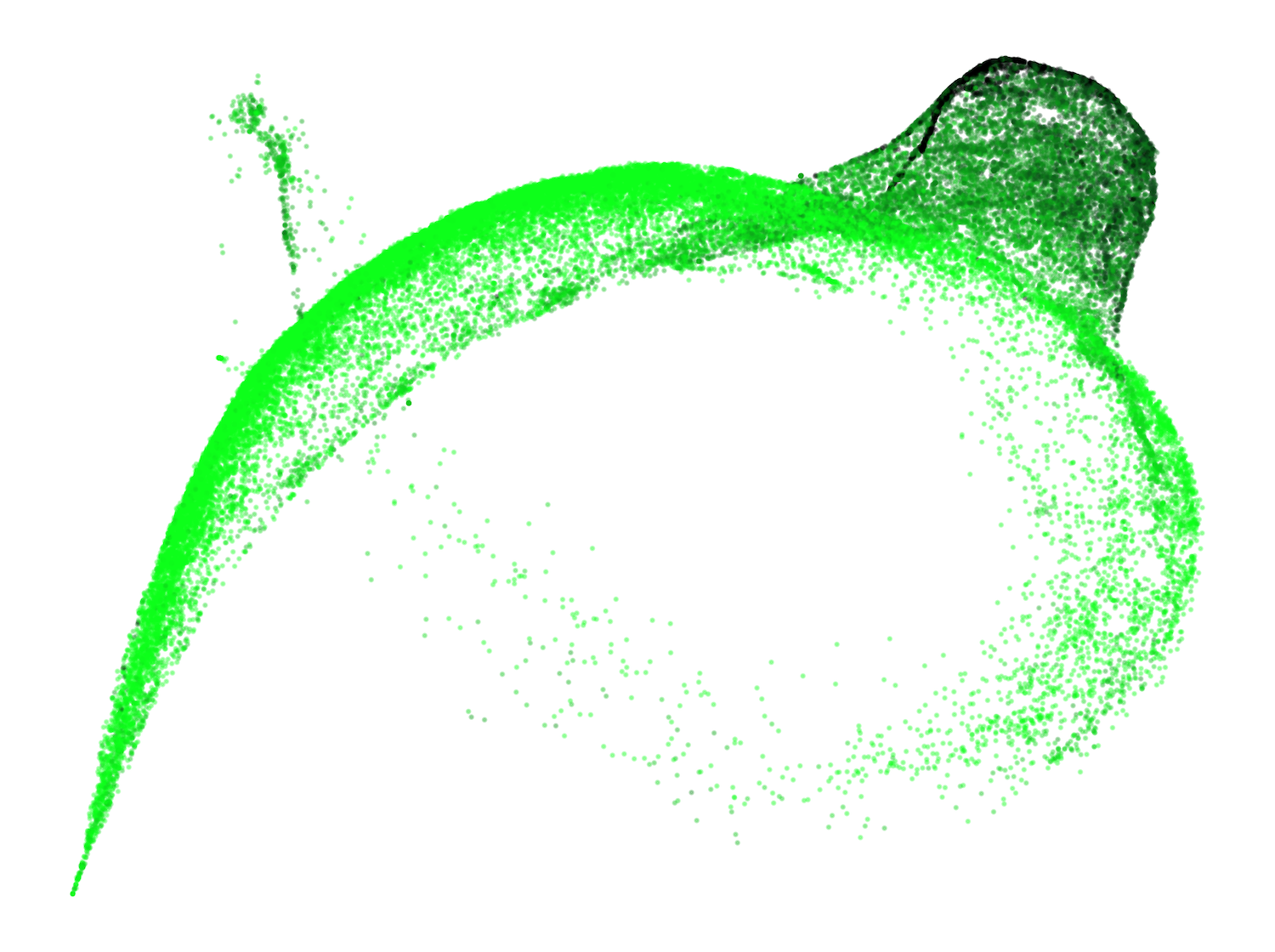
Figure 4: The development of the spacing fin: UMAP projections of spacing tokens colored by the number of preceding spacing tokens.

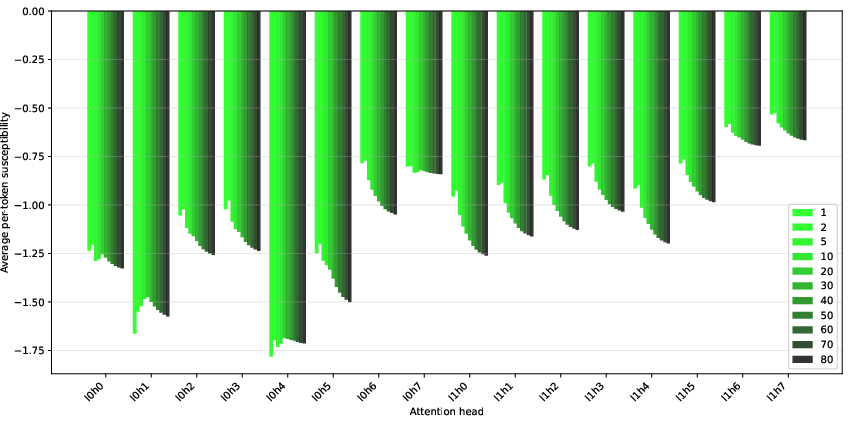
Figure 5: Average spacing token susceptibilities, conditional on the minimal number of preceding spacing tokens.

This structure suggests the model develops mechanisms for counting and differentiating spacing tokens, potentially distributed across multiple attention heads, and is influenced by the tokenizer's treatment of spaces.

Universality and Robustness Across Seeds

The developmental patterns observed are robust across multiple random seeds, with different initializations and minibatch orderings yielding highly similar UMAP structures and per-pattern susceptibility trajectories. While the specific heads assigned to functional roles (e.g., induction) vary, the high-level anatomical organization is preserved, indicating a degree of universality dictated by architecture and data distribution.

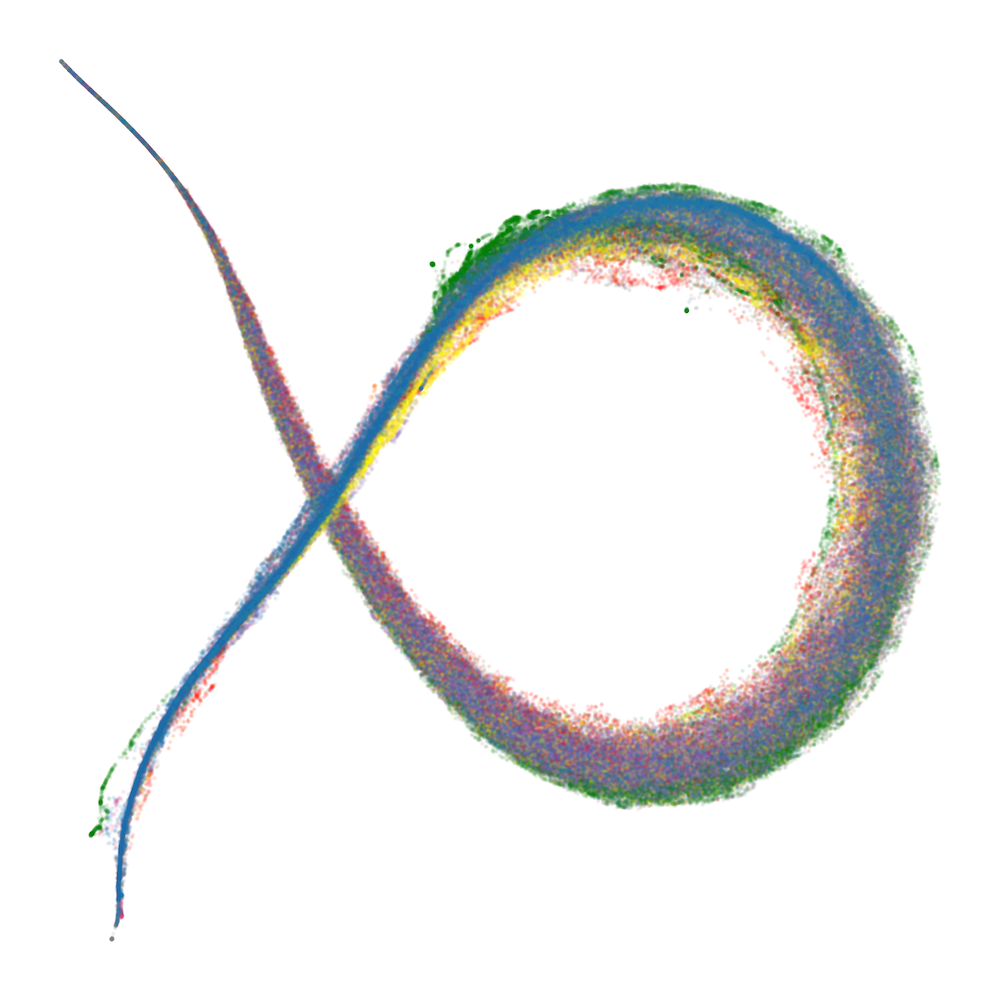
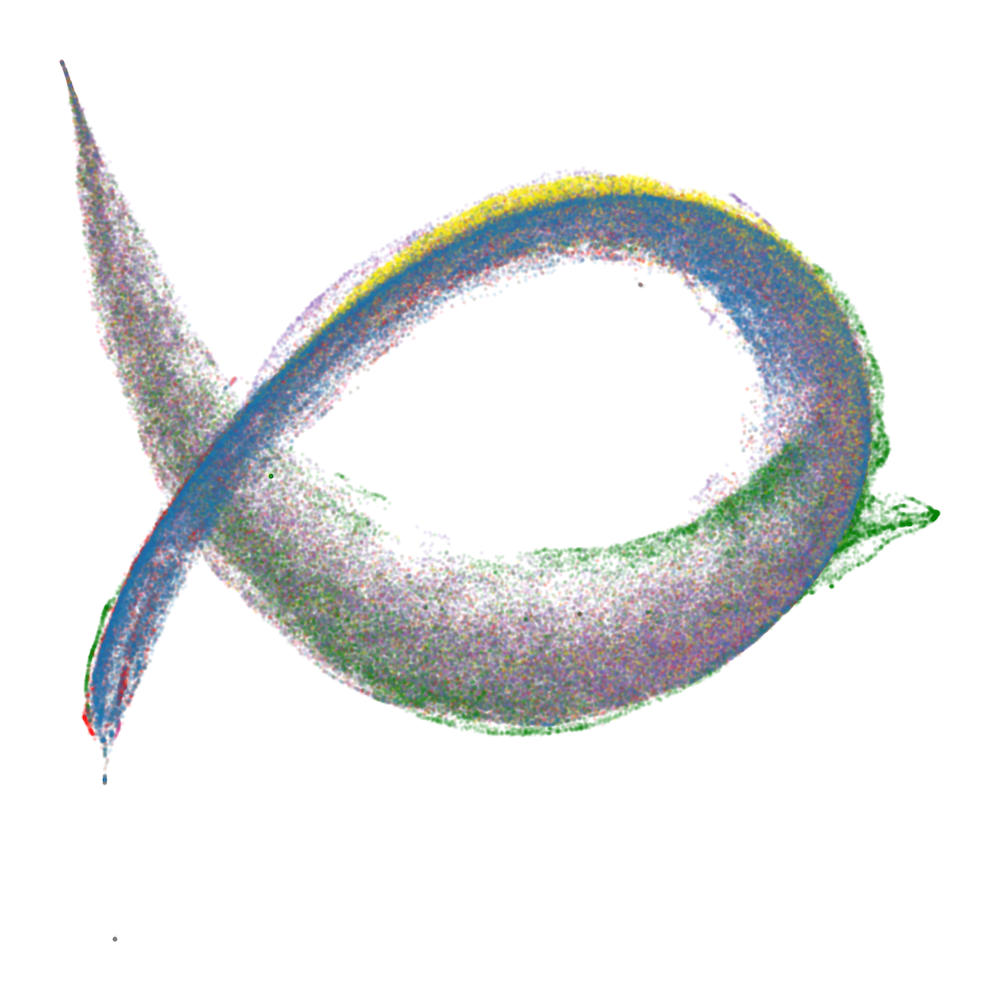
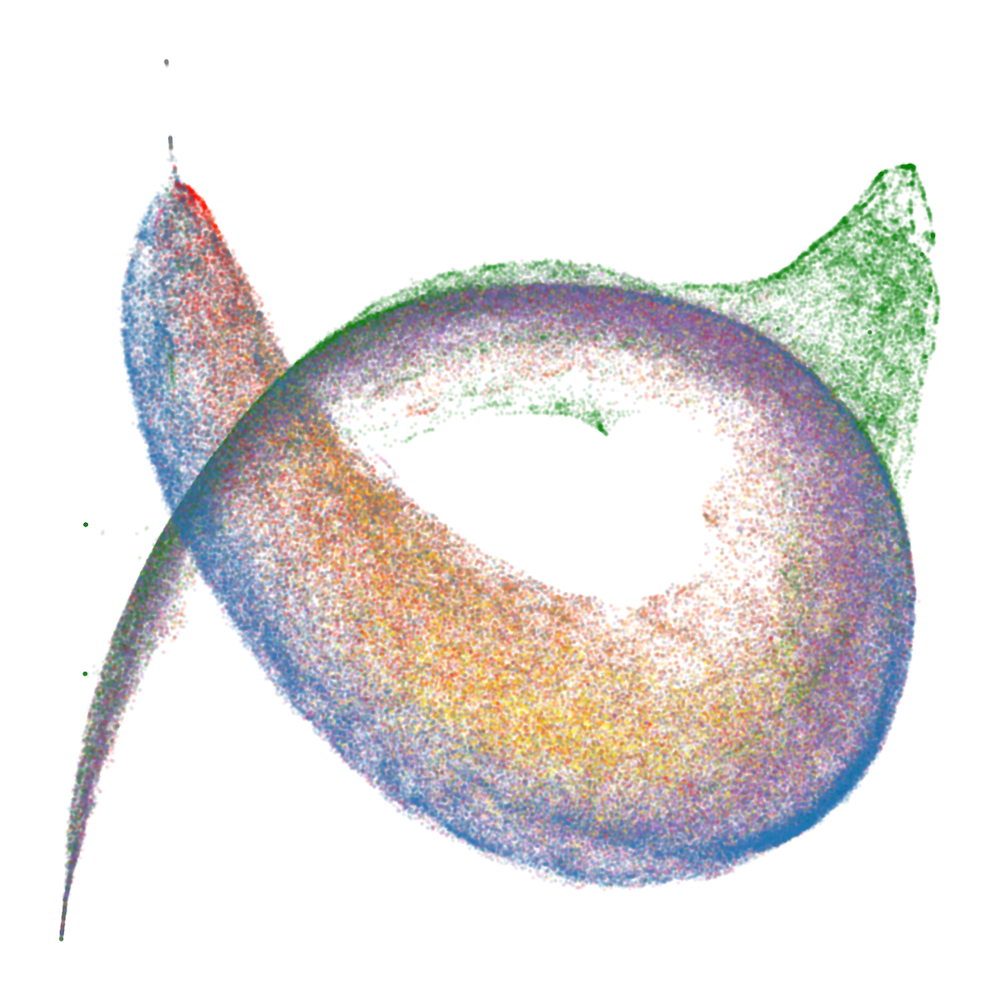
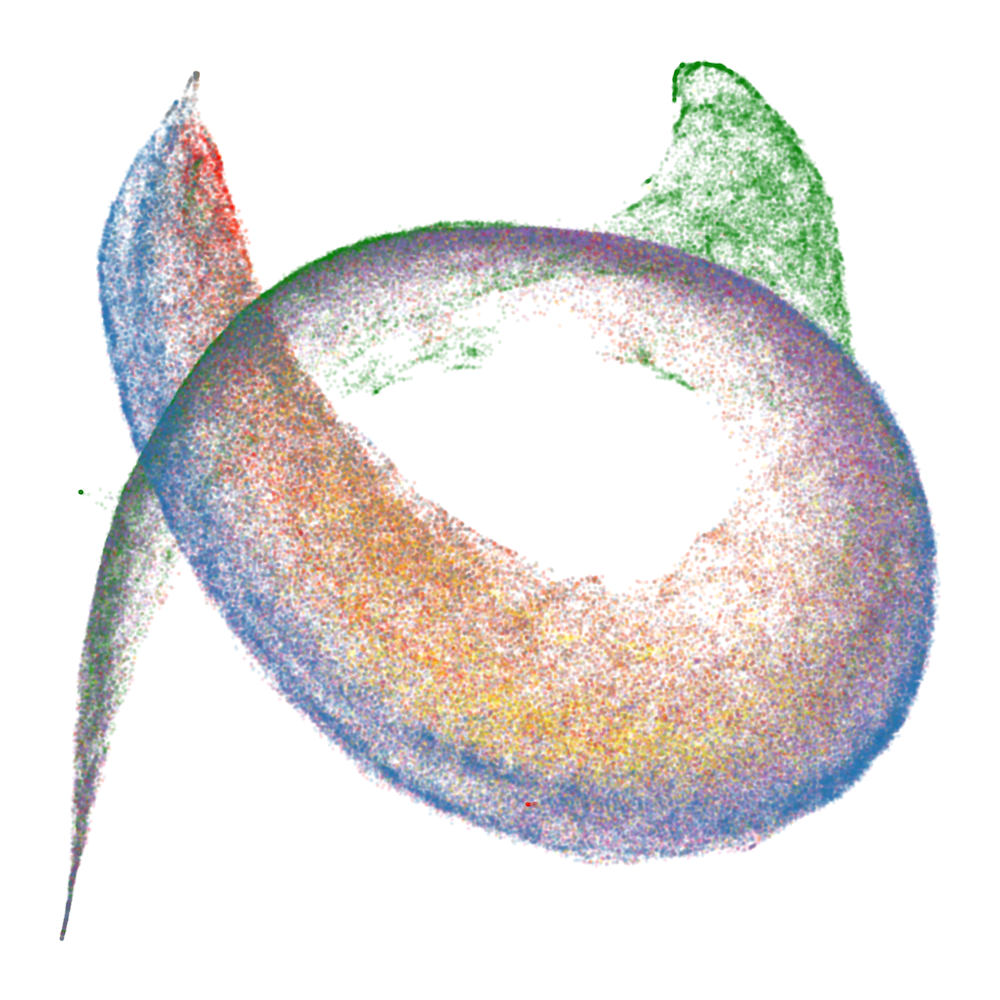
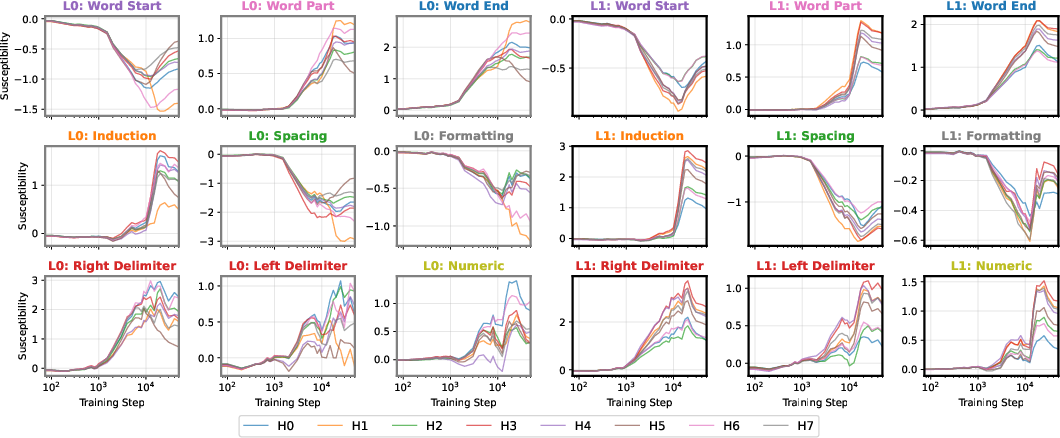
Figure 6: Embryology of the rainbow serpent, seed 2: UMAP projections and per-pattern susceptibilities across training.

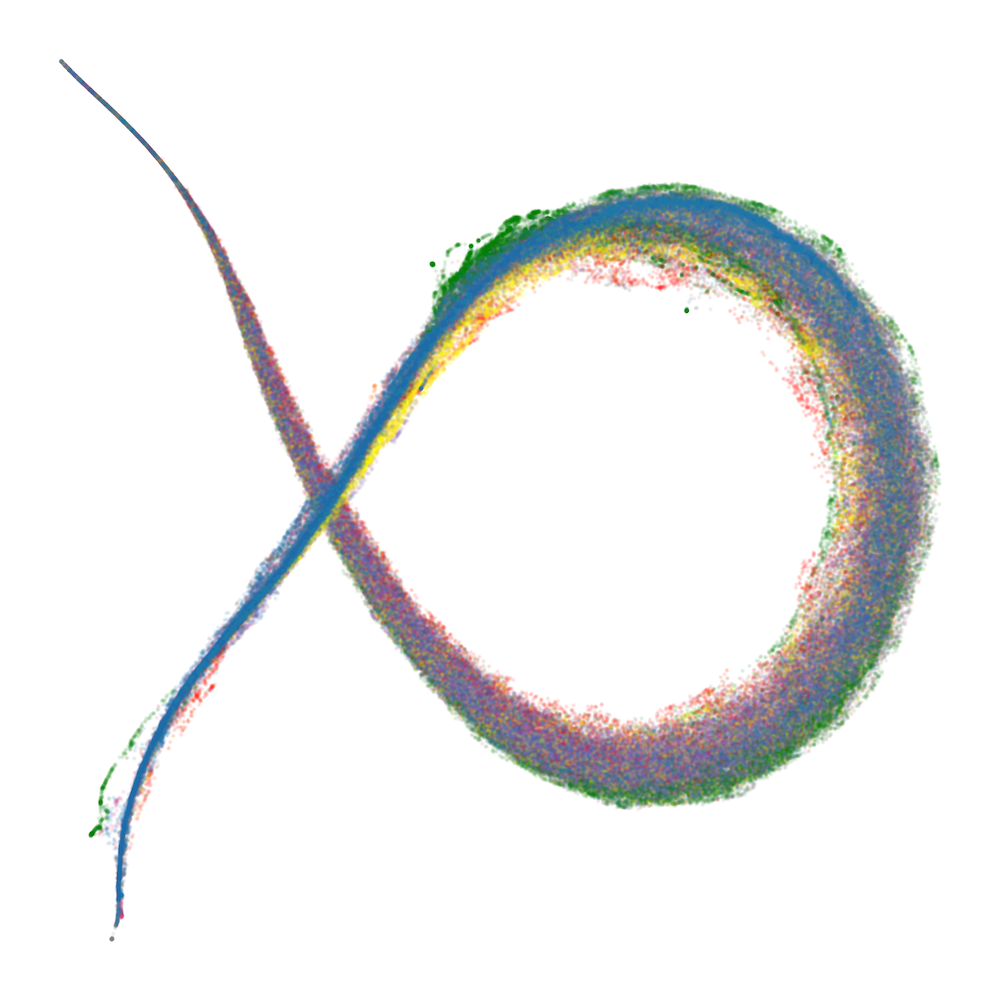
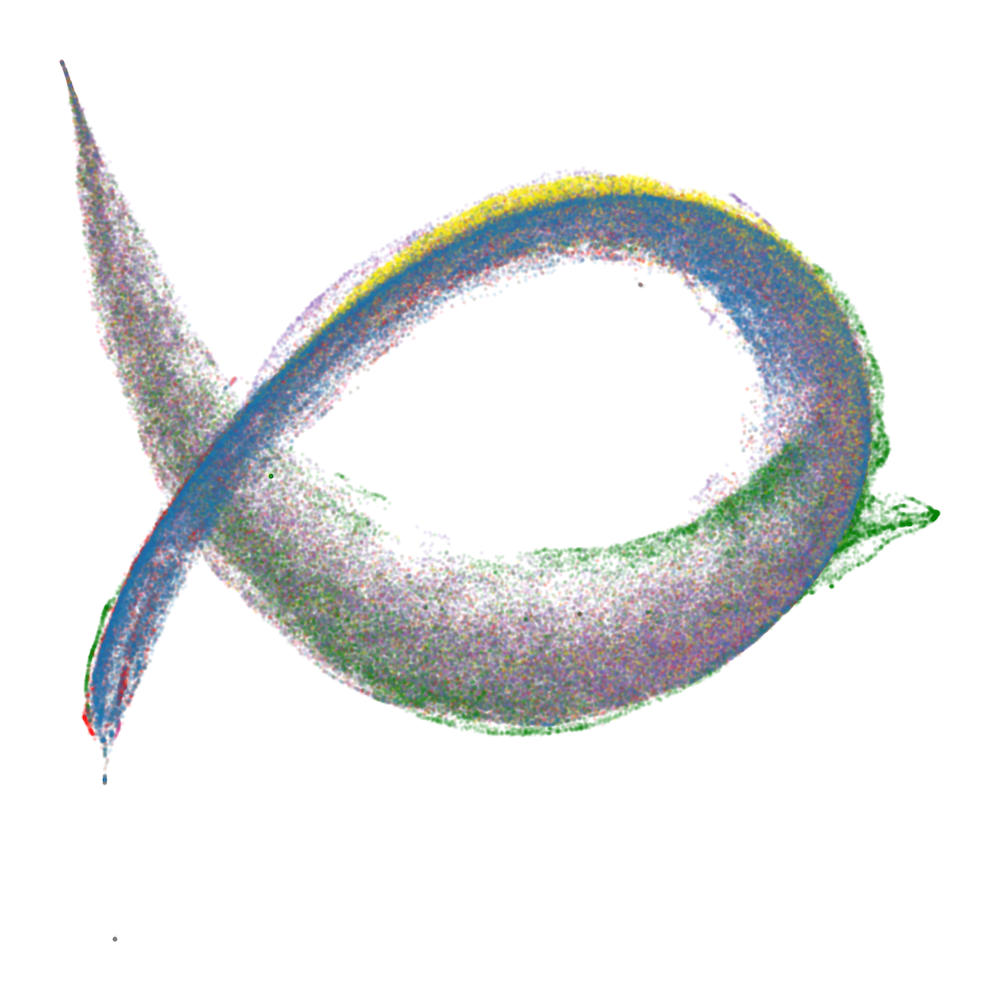
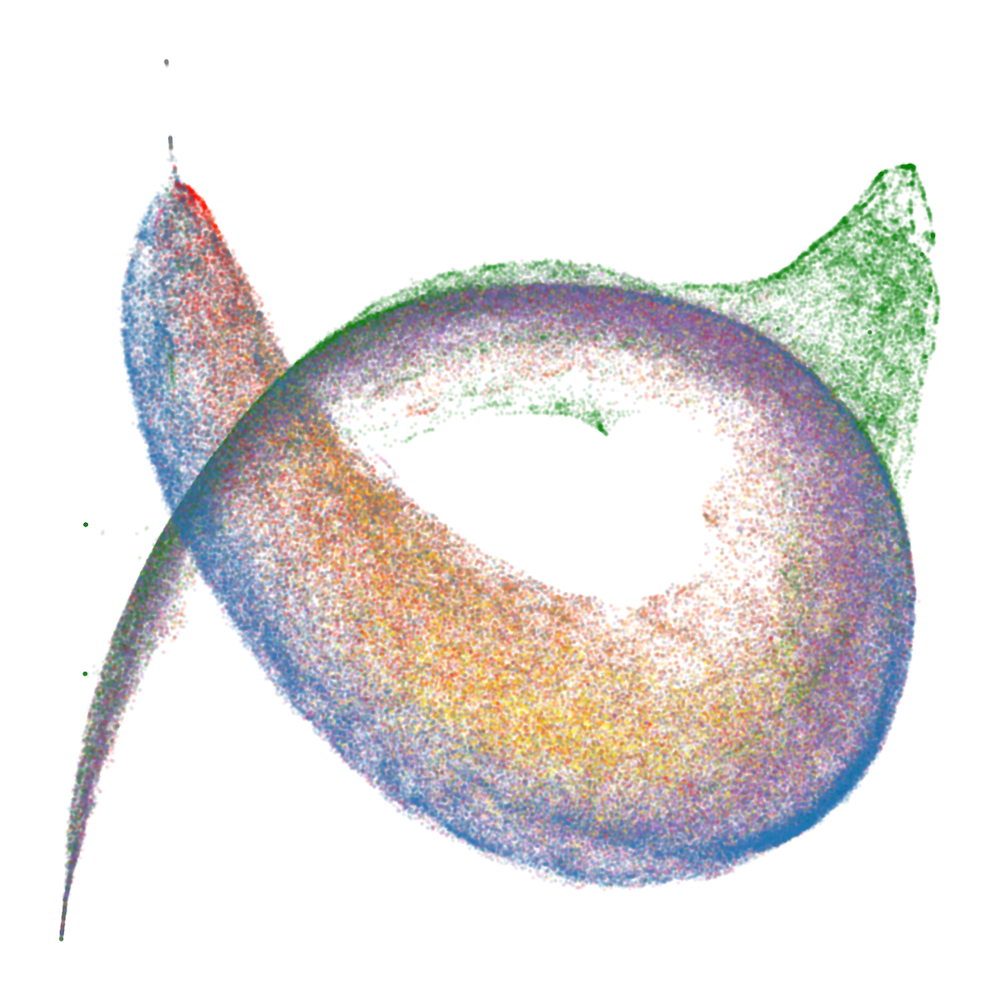
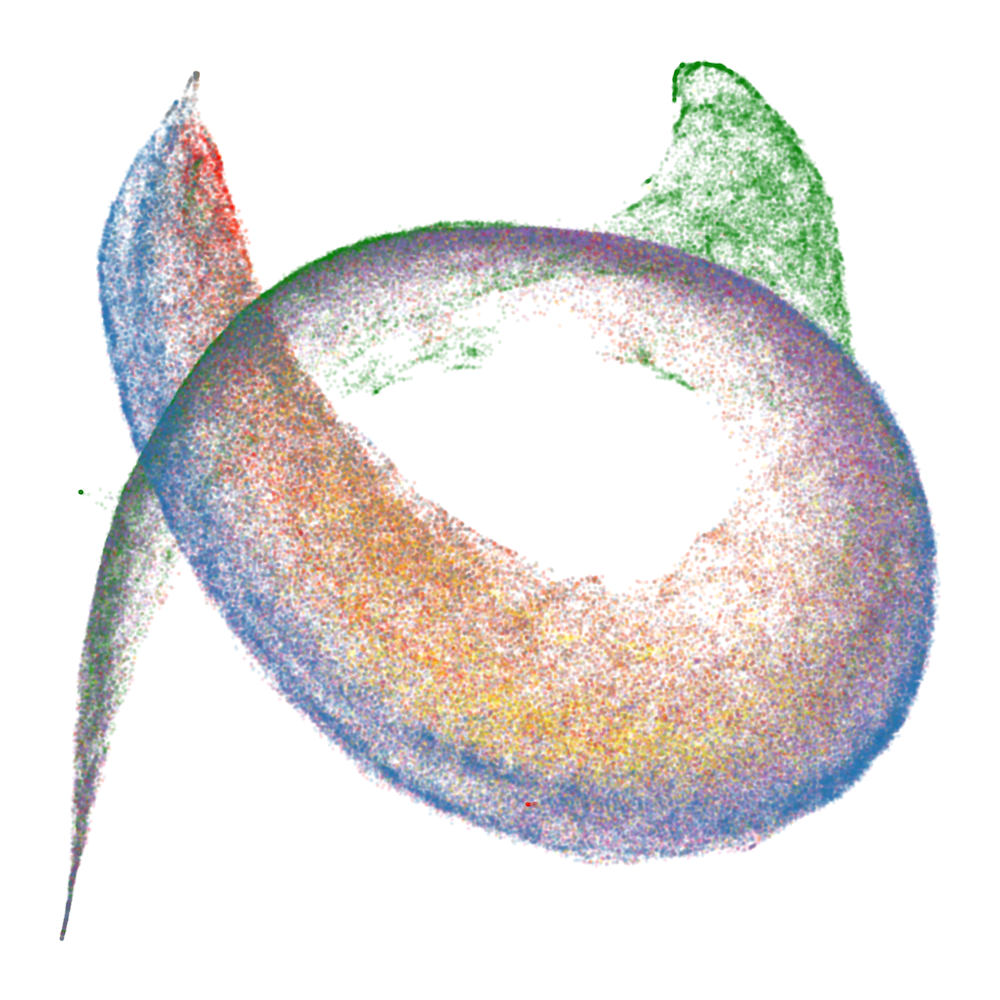
Figure 7: Embryology of the rainbow serpent, seed 3: UMAP projections and per-pattern susceptibilities across training.

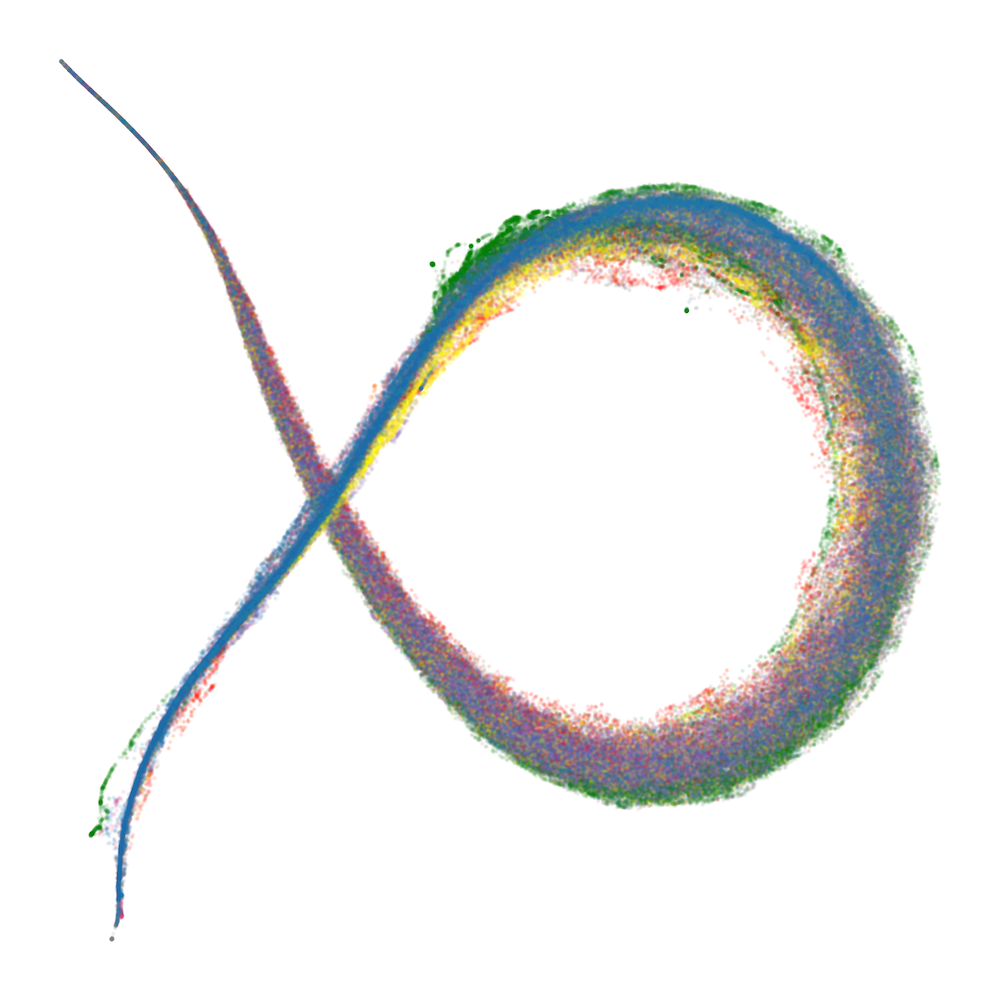
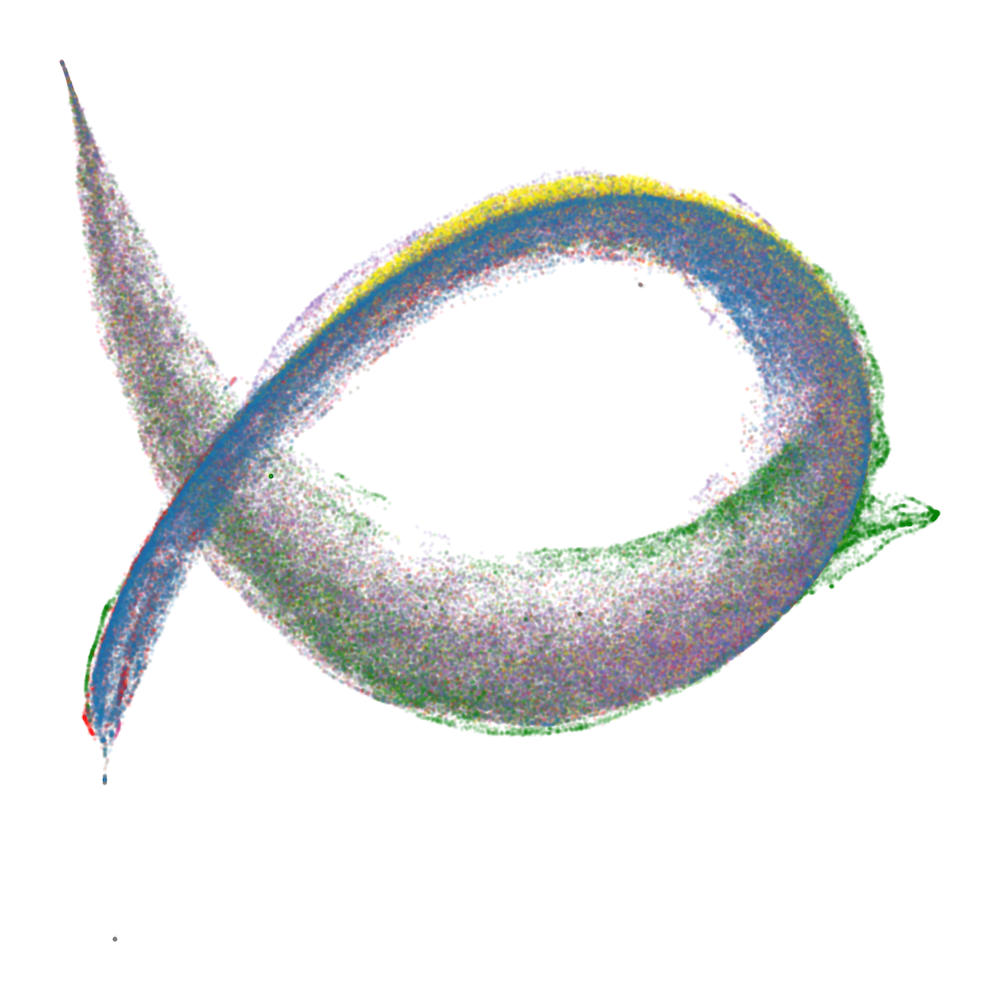
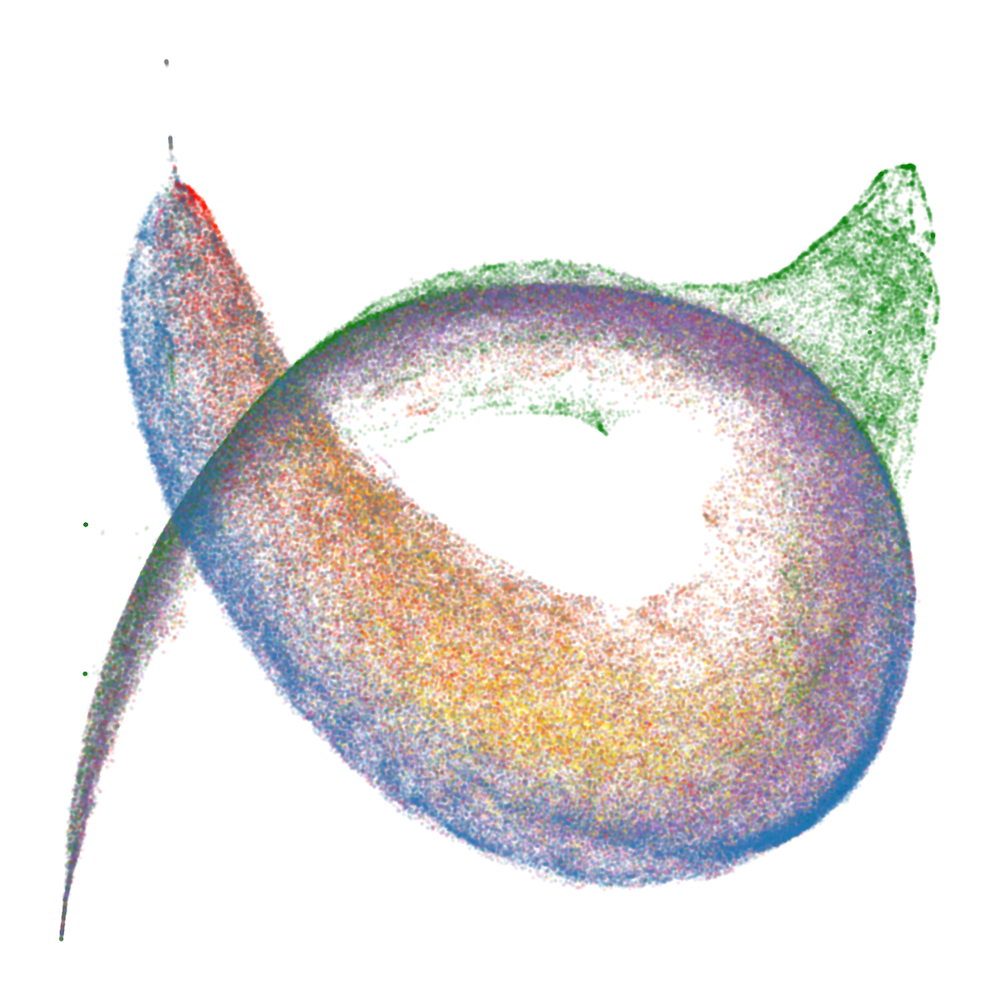
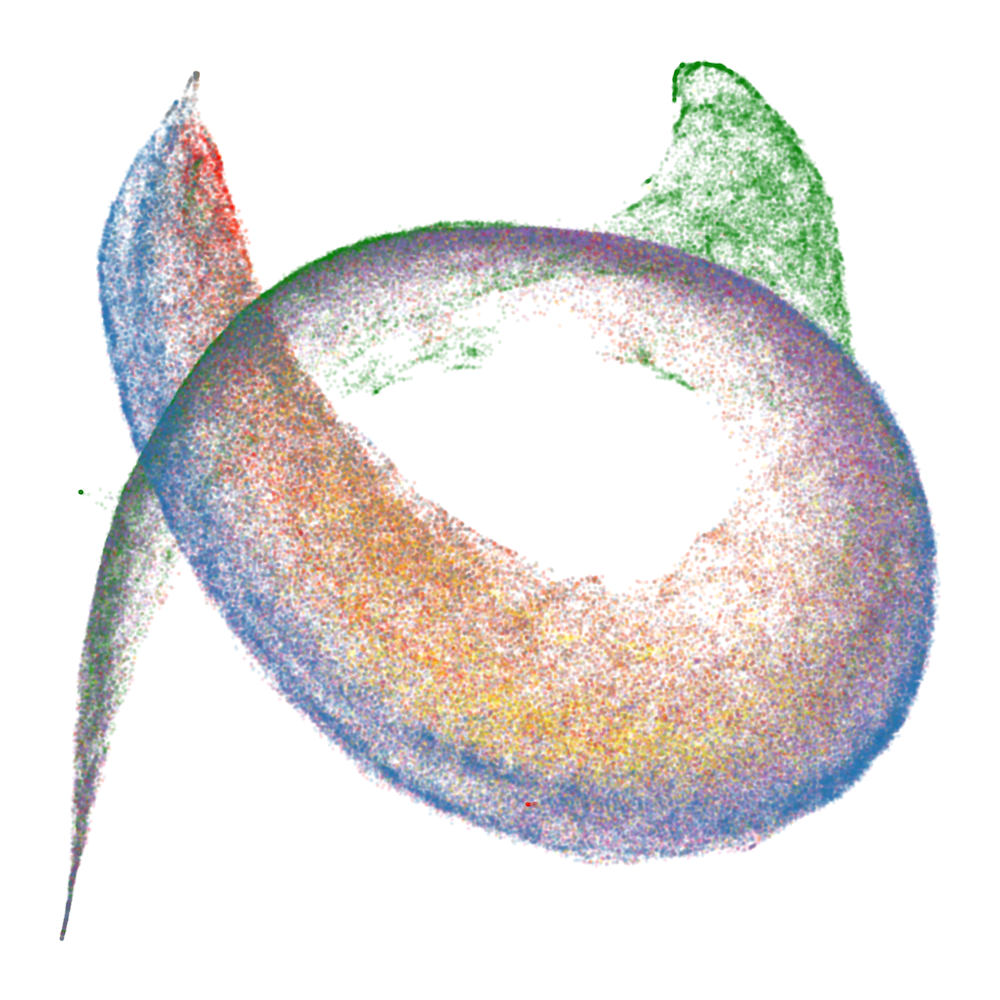
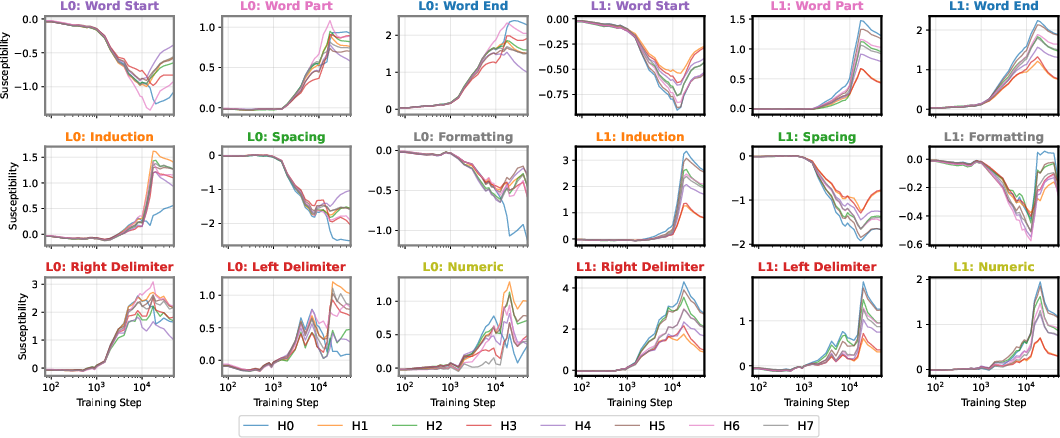
Figure 8: Embryology of the rainbow serpent, seed 4: UMAP projections and per-pattern susceptibilities across training.

Methodological Considerations

The choice of UMAP over PCA is justified by the preservation of non-linear structural information, such as the spacing fin and numeric token streaks, which are not captured by the first few principal components. The analysis focuses on large-scale phenomena robust to UMAP hyperparameters, avoiding artifacts due to local density distortions.

Theoretical and Practical Implications

The susceptibility-based approach provides a holistic lens for studying the developmental principles of neural networks, complementing circuit-centric mechanistic interpretability. Patterns of coordinated variation in susceptibilities across components are analogous to gene coexpression modules in genomics, enabling the identification of functional modules and their developmental trajectories.

The direct relationship between susceptibility patterns and generalization error, as formalized via singular learning theory and the local learning coefficient, links internal structure to generalization dynamics. The universality of the observed body plan across seeds suggests that certain organizational principles are intrinsic to the architecture and data, raising questions about the existence of fundamental "solution shapes" in LLMing.

Limitations and Future Directions

The paper is limited to a 3M parameter, two-layer attention-only transformer and a specific tokenizer. The prominence of the spacing fin is likely contingent on tokenization strategy. Whether susceptibility-based UMAP visualizations scale to larger models and alternative tokenizers remains an open question. Further mechanistic analysis of novel structures such as the spacing fin is warranted.

Conclusion

This work demonstrates that susceptibility analysis, combined with dimensionality reduction, enables the visualization and quantitative tracking of the developmental emergence of computational structure in LLMs. The approach recovers known circuits (e.g., induction) and uncovers novel mechanisms (e.g., spacing fin), with developmental trajectories exhibiting remarkable universality across seeds. The embryological perspective provides a new framework for understanding how neural networks organize and specialize during training, with implications for interpretability, generalization, and the science of deep learning.