A diffusion-based generative model for financial time series via geometric Brownian motion (2507.19003v1)

Abstract: We propose a novel diffusion-based generative framework for financial time series that incorporates geometric Brownian motion (GBM), the foundation of the Black--Scholes theory, into the forward noising process. Unlike standard score-based models that treat price trajectories as generic numerical sequences, our method injects noise proportionally to asset prices at each time step, reflecting the heteroskedasticity observed in financial time series. By accurately balancing the drift and diffusion terms, we show that the resulting log-price process reduces to a variance-exploding stochastic differential equation, aligning with the formulation in score-based generative models. The reverse-time generative process is trained via denoising score matching using a Transformer-based architecture adapted from the Conditional Score-based Diffusion Imputation (CSDI) framework. Empirical evaluations on historical stock data demonstrate that our model reproduces key stylized facts heavy-tailed return distributions, volatility clustering, and the leverage effect more realistically than conventional diffusion models.

• The paper introduces a diffusion model using GBM to inject multiplicative noise, effectively capturing market heteroskedasticity.
• The paper details a neural network featuring 1D convolutions, transformers, and gated residual modules to model long-range temporal dependencies.
• The paper demonstrates enhanced accuracy in reproducing heavy tails, volatility clustering, and the leverage effect compared to standard SDE methods.

Diffusion-Based Generative Modeling of Financial Time Series via Geometric Brownian Motion

Introduction and Motivation

The paper introduces a diffusion-based generative model for financial time series that explicitly incorporates geometric Brownian motion (GBM) into the forward noising process. This approach is motivated by the inadequacy of standard score-based diffusion models, which typically inject additive Gaussian noise and thus fail to capture the heteroskedastic, multiplicative nature of financial asset prices. By leveraging the GBM structure—central to the Black–Scholes framework—the model injects noise proportional to the asset price, aligning the generative process with empirically observed market dynamics such as heavy tails, volatility clustering, and the leverage effect.

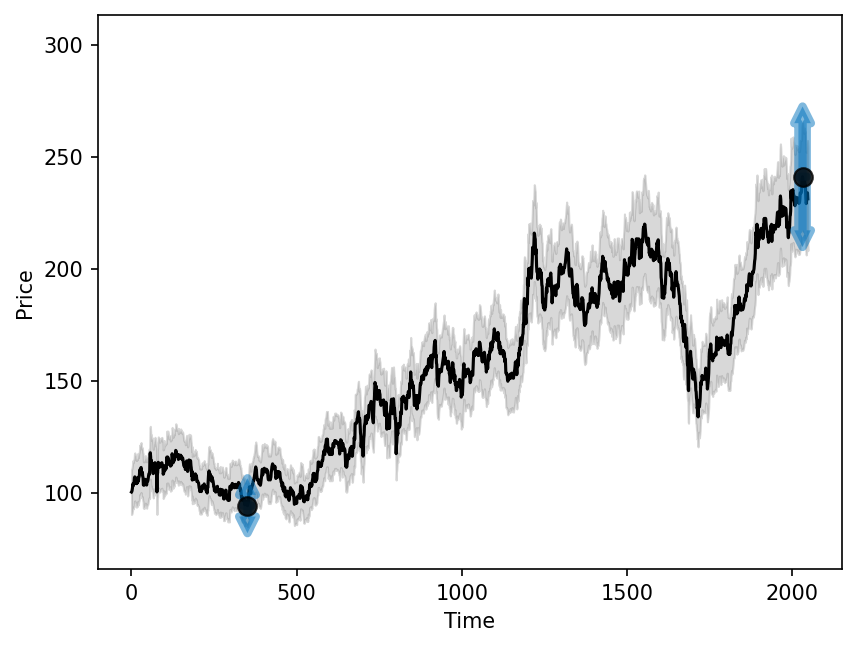
Figure 1: Generated price time series with a shaded envelope indicating price-dependent noise intensity. The width of the envelope reflects the level of uncertainty, which increases with the stock price.

Methodological Framework

GBM-Driven Forward SDE

The forward process is defined in log-price space, where the SDE for the log-price $X_t = \log S_t$ is given by:

$\mathrm{d}X_t = \sigma_t \, \mathrm{d}W_t$

with $\sigma_t$ as a time-dependent noise schedule. This is a variance-exploding (VE) SDE, but crucially, the exponential mapping back to price space induces state-dependent volatility, a key property of real financial time series.

The model's forward process thus differs fundamentally from standard VE/VP SDEs by introducing multiplicative noise in price space, which is essential for capturing heteroskedasticity and the empirically observed scaling of volatility with price.

Score Network Architecture

The reverse-time generative process is parameterized by a neural network adapted from the Conditional Score-based Diffusion Imputation (CSDI) framework. The architecture integrates:

• 1D convolutional layers for local feature extraction,
• Transformer blocks for modeling long-range temporal dependencies,
• Gated residual modules and skip connections for stable training and hierarchical representation,
• Explicit temporal, positional, and diffusion-step embeddings to encode time, sequence position, and noise level.

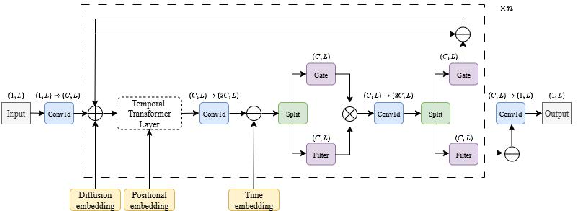
  Figure 2: Neural network architecture based on CSDI used for score estimation. The network consists of convolutional layers, transformer blocks, gated residual modules, and skip connections to model financial time series data.

Empirical results demonstrate that increasing the model's representational capacity—specifically, the dimensionality of convolutional channels and embeddings—substantially improves the ability to capture asymmetric dependencies such as the leverage effect.

Figure 3: Leverage effect across three different neural network configurations (rows) and noise schedules (columns).

Data and Training Protocol

The model is trained on daily log-returns of S&P 500 constituents with at least 40 years of historical data, using a sliding window approach to extract subsequences of length 2048. The score network is trained via denoising score matching, with the forward process discretized into 2000 steps and a minibatch size of 64.

Empirical Evaluation

Stylized Facts: Heavy Tails, Volatility Clustering, Leverage Effect

The model is evaluated on its ability to reproduce three canonical stylized facts of financial time series:

1. Heavy-tailed return distributions: Empirical return distributions exhibit power-law decay with tail exponents $\alpha$ in the range $3 \leq \alpha \leq 5$.
2. Volatility clustering: The autocorrelation of absolute returns decays slowly, indicating long-range dependence.
3. Leverage effect: Negative returns are followed by increased future volatility, manifesting as a negative lead–lag correlation.

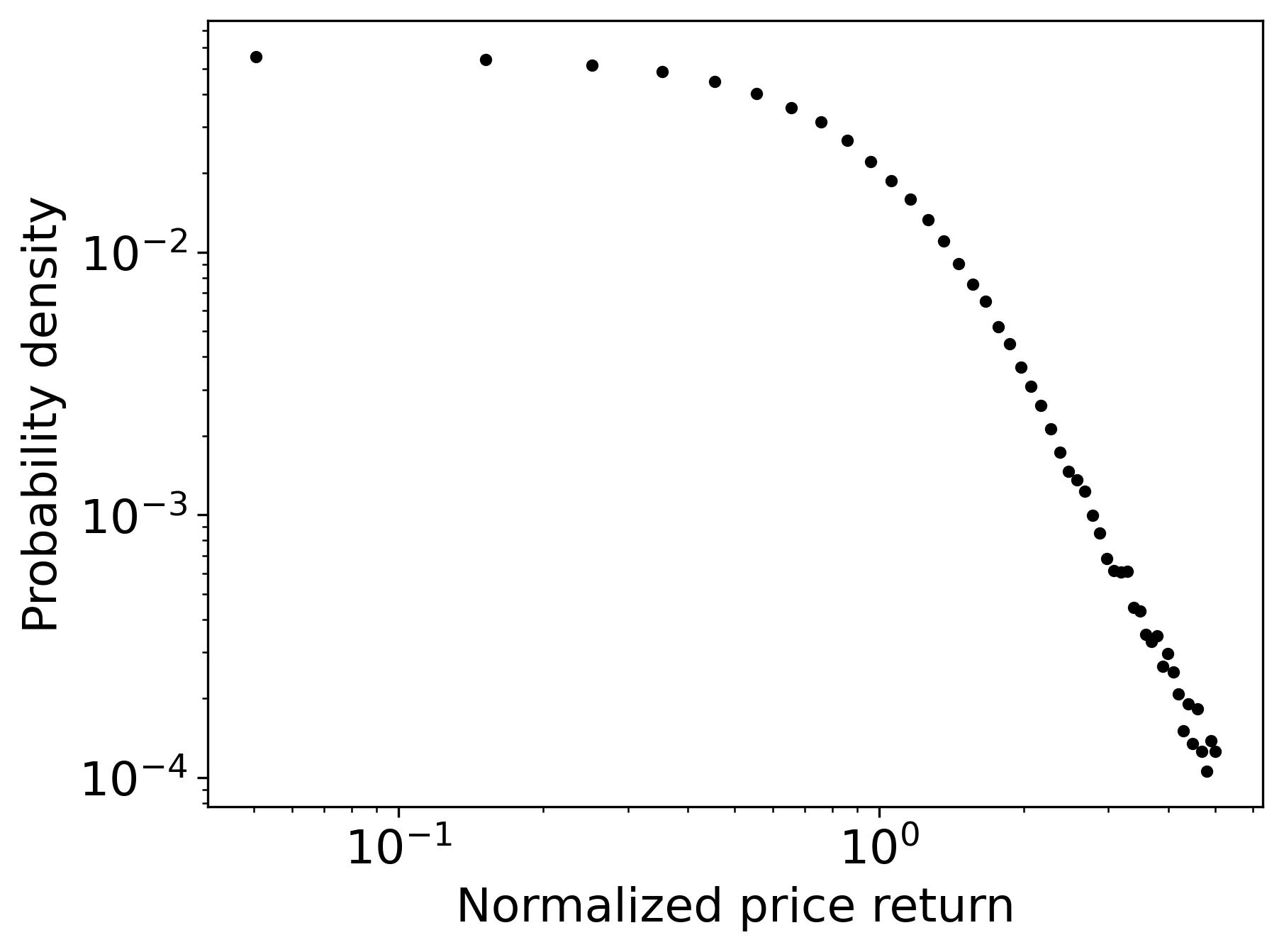
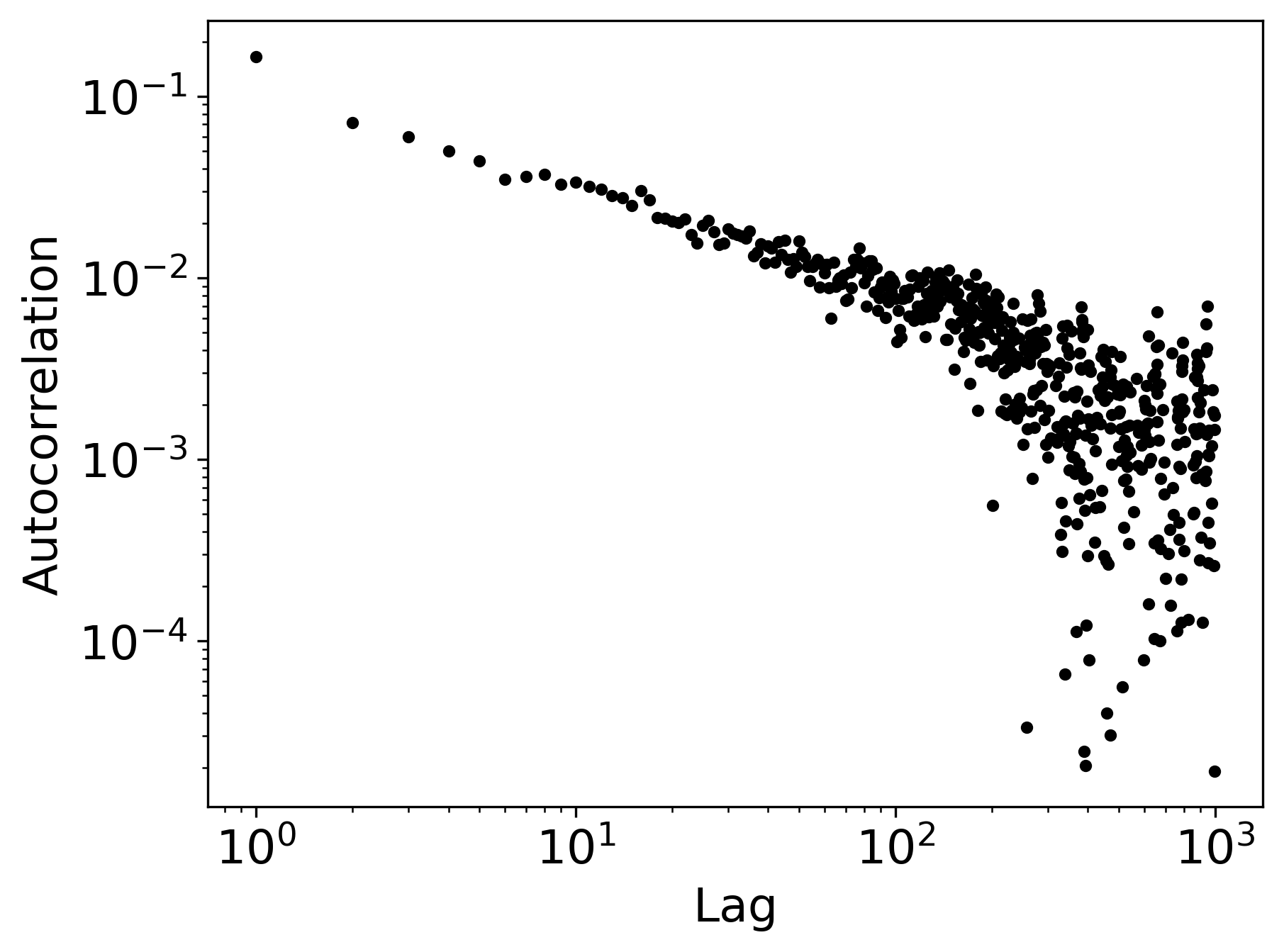
Figure 4: Heavy-tail distribution with $\alpha=4.35$.

Figure 5: Volatility clustering across three SDE variants (rows) under different noise schedules (columns).

Figure 6: Leverage effect across three SDE variants (rows) and noise schedules (columns).

Comparative Analysis: SDE Variants and Noise Schedules

The paper systematically compares the GBM-based SDE with standard VE and VP SDEs under linear, exponential, and cosine noise schedules. Key findings include:

• GBM SDE with exponential or cosine noise schedules yields tail exponents ($\alpha$) closest to empirical values, accurately reproducing heavy tails.
• Volatility clustering is best captured by the GBM SDE, with autocorrelation decay patterns closely matching real data.
• Leverage effect is robustly reproduced only by the GBM SDE, especially with increased model capacity and appropriate noise scheduling.

Standard VE/VP SDEs, lacking multiplicative noise, consistently underestimate tail heaviness and fail to capture volatility clustering and leverage asymmetry.

GAN Baseline Comparison

The GBM-based diffusion model is benchmarked against a GAN-based approach [takahashi2019modeling]. While both models can reproduce heavy tails, the GBM-diffusion model demonstrates superior fidelity in volatility clustering and leverage effect, with smoother, more persistent autocorrelation and negative lead–lag correlation patterns.

Theoretical and Practical Implications

The integration of GBM into the forward noising process constitutes a principled inductive bias, directly embedding financial-theoretic structure into the generative model. This approach addresses the limitations of generic diffusion models and GANs, which lack domain-specific structure and often fail under distributional shift or market stress.

Practical implications include:

• Generation of realistic synthetic financial time series for risk modeling, stress testing, and data augmentation,
• Improved scenario generation for derivative pricing and portfolio management, leveraging the model's consistency with Black–Scholes theory,
• Enhanced interpretability and robustness due to the explicit modeling of state-dependent volatility.

Theoretical implications involve a paradigm shift from modeling price dynamics directly to modeling the noise process, opening avenues for further integration of financial SDEs and stochastic volatility models into deep generative frameworks.

Limitations and Future Directions

A notable limitation is the departure from exact log-normality in marginal price distributions, as the model generates entire trajectories rather than simulating a Markovian process with time-consistent marginals. Addressing this may require explicit Markovian inductive bias or latent volatility processes.

Future research directions include:

• Incorporation of stochastic or rough volatility structures,
• Conditioning on macroeconomic or implied volatility features,
• Application to market simulation, stress testing, and supervised learning in quantitative finance.

Conclusion

The proposed GBM-based diffusion model for financial time series generation demonstrates clear advantages over standard diffusion and GAN-based models in reproducing key empirical properties of asset returns. By embedding financial-theoretic priors into the generative process, the model achieves both statistical fidelity and interpretability, providing a robust foundation for synthetic data generation and downstream financial applications. The approach represents a significant methodological advance in the intersection of deep generative modeling and financial mathematics, with broad implications for both research and practice.