Temporal Entanglement from Holographic Entanglement Entropy (2507.17847v2)

Abstract: Recently, several notions of entanglement in time have emerged as a novel frontier in quantum many-body physics, quantum field theory and gravity. We propose a systematic prescription to characterize temporal entanglement in relativistic quantum field theory in a general state for an arbitrary subregion on a flat, constant-time slice in a flat spacetime. Our prescriptions starts with the standard entanglement entropy of a spatial subregion and amounts to transporting the unchanged subregion to boosted time slices all the way across the light cone when it becomes in general a complex characterization of the corresponding temporal subregion. For holographic quantum field theories, our prescription amounts to an analytic continuation of all codimension-two bulk extremal surfaces satisfying the homology constraint and picking the one with the smallest real value of the area as the leading saddle point. We implement this prescription for holographic conformal field theories in thermal states on both a two-dimensional Lorentzian cylinder and three-dimensional Minkowski space, and show that it leads to results with self-consistent physical properties of temporal entanglement.

• The paper introduces a prescription that uses analytic continuation and holographic extremal surfaces to define temporal entanglement entropy in strongly coupled QFTs.
• It reveals phase transitions and multiple saddle contributions, illustrating a shift from vacuum-connected to horizon-connected branches near the light cone.
• The approach respects the UV-IR correspondence and strong subadditivity, ensuring that the method remains consistent with standard QFT and holographic expectations.

Temporal Entanglement from Holographic Entanglement Entropy: A Technical Analysis

Introduction and Motivation

The paper "Temporal Entanglement from Holographic Entanglement Entropy" (2507.17847) addresses the formalization and computation of temporal (timelike) entanglement entropy in relativistic quantum field theory (QFT), with a focus on holographic (AdS/CFT) settings. While spatial entanglement entropy is well-understood and underpins much of modern quantum information and holography, the extension to temporal entanglement is nontrivial due to the lack of a canonical notion of "entanglement in time" in standard quantum mechanics and QFT. The work builds on recent developments in tensor networks, pseudoentropy, and analytic continuation techniques, proposing a systematic prescription for defining and computing temporal entanglement entropy, particularly in strongly coupled, large-$N$ QFTs with holographic duals.

Prescription for Temporal Entanglement Entropy

The central proposal is to define temporal entanglement entropy via analytic continuation of the standard spatial entanglement entropy. The procedure involves:

1. Geometric Rotation of Subregions: Starting from a spatial subregion on a constant-time slice, the region is "rotated" in the $(t, x)$ plane by an angle $\theta$, interpolating between spacelike ($\theta=0$) and timelike ($\theta=\pi/2$) separations. The light cone is crossed at $\theta = \pi/4$.
2. Analytic Continuation Across the Light Cone: To avoid the singularity at the light cone (where the proper size of the subregion vanishes), the rotation is complexified, detouring infinitesimally into the complex $\theta$-plane. This is analogous to the $i\epsilon$ prescription in real-time QFT.
3. Holographic Implementation: In AdS/CFT, the entanglement entropy is computed via the area of codimension-two extremal surfaces anchored to the boundary subregion. The prescription requires analytic continuation of all such extremal surfaces (including complex saddles) that satisfy the homology constraint, followed by selection of the surface with the minimal real part of the area as the dominant contribution.

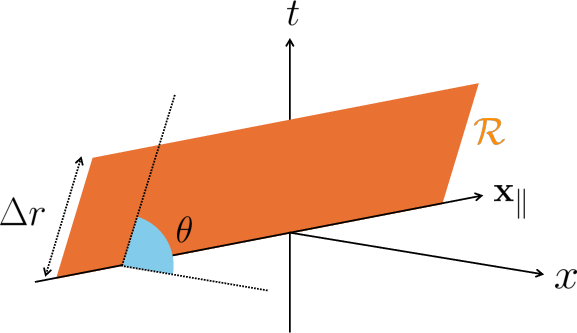
   Figure 1: Geometry of a strip boundary subregion $\mathcal{R}$ in three-dimensional Minkowski space, illustrating the rotation in the $t$-$x$ plane at fixed coordinate extent $\Delta r$.

This approach generalizes the Ryu-Takayanagi and Hubeny-Rangamani-Takayanagi prescriptions to temporal subregions and provides a concrete operational definition of temporal entanglement entropy in holographic QFTs.

Holographic Analysis: Black Brane and BTZ Geometries

Black Brane in $\mathbb{R}^{1,2}$

The authors analyze a four-dimensional AdS black brane geometry, dual to a thermal state in a three-dimensional CFT, with a strip subregion on the boundary. The extremal surfaces are parametrized by the tip position $z_t$ in the bulk. For spacelike strips ($\theta=0$), there is a unique real extremal surface for each width $\Delta r$.

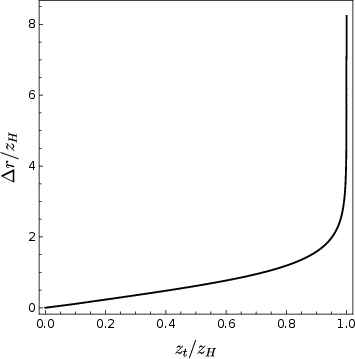
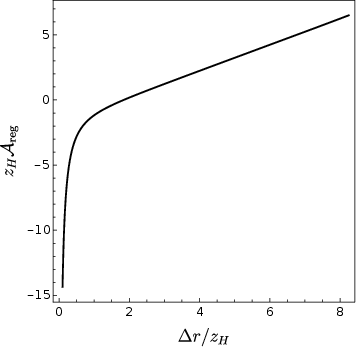
Figure 2: Left: Width of the strip $\Delta r$ as a function of the tip position $z_t$. Right: Regularized area density $\mathcal{A}_{\mathrm{reg}}$ as a function of $\Delta r$.

As $\theta$ approaches the light cone, a first-order phase transition occurs in the entanglement entropy, corresponding to a discontinuous jump in the dominant extremal surface from a vacuum-connected to a horizon-connected branch. This is reflected in the non-monotonicity of $\Delta r(z_t)$ and the emergence of multiple real and complex extremal surfaces.

Figure 3: For a strip with $\theta=\frac{\pi}{2}$, the complex $z_t$-plane structure of extremal surfaces, showing vacuum-connected (blue) and vacuum-disconnected (green) branches.

Upon analytic continuation to the timelike regime ($\theta > \pi/4$), the prescription tracks the analytic continuation of all real extremal surfaces, resulting in a set of complex extremal surfaces. The dominant contribution to the timelike entanglement entropy is always given by the analytic continuation of the vacuum-connected branch for all $\Delta r < \Delta r_{\mathrm{min}}^\star$, ensuring consistency with the UV-IR correspondence. For larger $\Delta r$, vacuum-disconnected branches become available but are always subdominant in the real part of the area, except in a narrow regime near the light cone where a zeroth-order phase transition can occur.

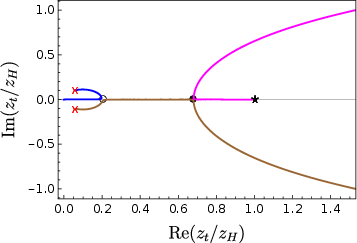
Figure 4: Relevant branches of complex extremal surfaces for $\theta = \frac{\pi}{4}-10^{-4}-10^{-6}i$, illustrating the rearrangement of real and complex branches near the light cone.

Figure 5: Complex $z_t$-plane trajectories of extremal surfaces under analytic continuation for various $\Delta r/z_H$, showing the mapping from real to complex branches.

BTZ Black Hole and Conical Defect in $\mathbb{R} \times S^1$

The analysis is extended to three-dimensional bulk geometries (BTZ black hole and conical defect), dual to thermal and excited states of a two-dimensional CFT on a Lorentzian cylinder. Here, the entangling region is an interval with endpoints separated by $(\Delta t, \Delta \phi)$. The compactness of the spatial direction introduces additional kinematical singularities when the endpoints become null-separated via the spatial circle.

The prescription correctly reproduces the expected light cone singularities in the entanglement entropy, both for the subregion and its complement, and ensures that the analytic continuation and minimization over saddles are performed in the correct order. This is essential for capturing all kinematical singularities and for consistency with field theory expectations.

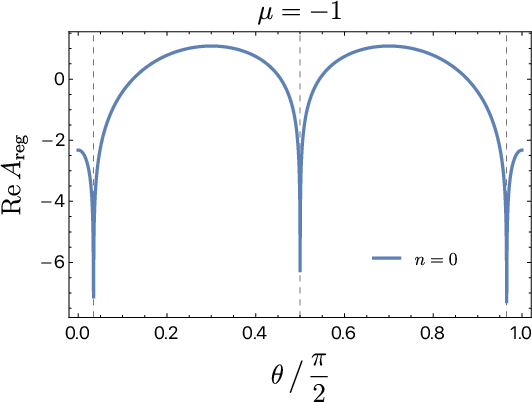
Figure 6: Analytic continuation of holographic entanglement entropy in the vacuum state, $\mu=-1$, for $\Delta r=1.9\pi > \pi\sqrt{2}$, showing kinematical singularities as a function of the rotation angle $\theta$.

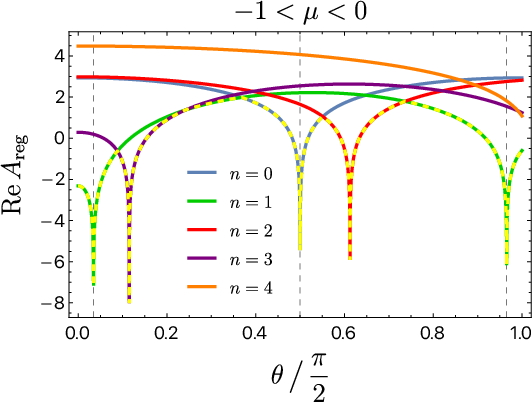
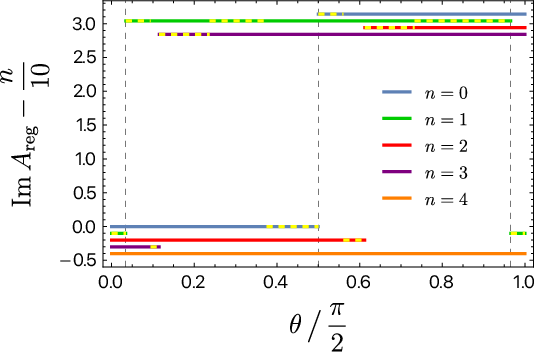
Figure 7: Analytic continuation in the excited state (conical defect), $-1<\mu<0$, with additional bulk singularities and multiple winding geodesics.

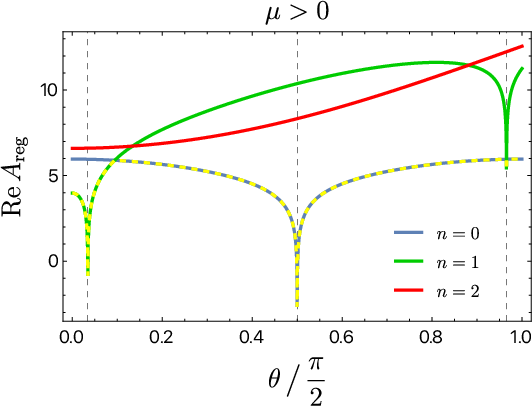
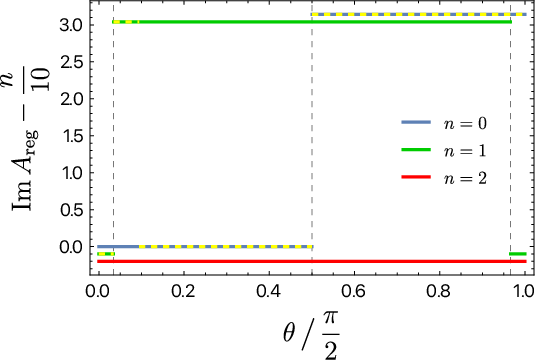
Figure 8: Analytic continuation in the thermal state (BTZ black hole), $\mu>0$, with homology constraint enforced and dominant configurations highlighted.

Technical Implications and Numerical Results

• Dominance of Analytically Continued Saddles: The prescription ensures that only those complex extremal surfaces that are analytic continuations of real saddles in the spacelike regime contribute to the timelike entanglement entropy. This avoids unphysical contributions from "vacuum-disconnected" branches that do not reduce to the vacuum answer in the small interval limit.
• Non-commutativity of Minimization and Analytic Continuation: The order of operations—analytic continuation followed by minimization—is crucial. Minimizing before analytic continuation can miss kinematical singularities and lead to incorrect physical behavior.
• Phase Transitions: Both first-order and zeroth-order phase transitions in the entanglement entropy are observed as a function of interval size and rotation angle, reflecting the intricate structure of the extremal surface landscape.
• UV-IR Correspondence: The prescription is constructed to respect the UV-IR correspondence, ensuring that for small temporal subregions, the result reduces to the vacuum answer, as required by consistency with QFT.
• Strong Subadditivity: The minimization over the real part of the area among analytically continued surfaces leads to strong subadditivity of the timelike entanglement entropy, provided the real part is nonzero.

Theoretical and Practical Implications

The work provides a robust, operational definition of temporal entanglement entropy in holographic QFTs, resolving ambiguities associated with multiple complex extremal surfaces and ensuring consistency with field-theoretic and geometric expectations. The prescription is general and can be applied to arbitrary states and subregions in flat spacetimes, and is readily extendable to more general holographic setups.

Practically, the method enables explicit computation of timelike entanglement entropy in strongly coupled QFTs where direct field-theoretic calculations are intractable. The approach is amenable to numerical implementation, as the analytic continuation and minimization can be performed for extremal surfaces obtained via standard shooting or relaxation methods in the bulk.

Theoretically, the results clarify the role of complex extremal surfaces in holography, the structure of phase transitions in entanglement entropy, and the interplay between analytic continuation and saddle point dominance. The findings also have implications for the paper of information-theoretic properties in time-dependent and out-of-equilibrium settings, and for the understanding of causal structure and singularities in AdS/CFT.

Future Directions

• Extension to Higher Dimensions and Nontrivial Topologies: The prescription can be applied to higher-dimensional CFTs and more complicated subregion geometries, potentially revealing new phenomena in temporal entanglement.
• Tensor Network and Lattice Implementations: The analytic continuation approach may be adapted to tensor network simulations and lattice models, enabling the paper of temporal entanglement in discrete systems and its relation to holography.
• Connections to Quantum Information and Complexity: The formalism may shed light on the role of temporal entanglement in quantum information processing, operator growth, and quantum complexity.
• Generalization Beyond the Cylinder: The limitation to intervals of size less than the spatial circle in the cylinder case suggests further generalization is possible, potentially connecting to recent proposals for observable and computable entanglement in time.

Conclusion

The paper establishes a systematic, physically consistent prescription for temporal entanglement entropy in relativistic QFTs, with a concrete holographic implementation. By leveraging analytic continuation of entangling regions and extremal surfaces, and by carefully ordering analytic continuation and minimization, the approach resolves longstanding ambiguities and provides a powerful tool for exploring temporal entanglement in strongly coupled systems. The results have broad implications for holography, quantum information, and the paper of time-dependent phenomena in QFT.