Time Deep Gradient Flow Method for pricing American options (2507.17606v1)

Abstract: In this research, we explore neural network-based methods for pricing multidimensional American put options under the BlackScholes and Heston model, extending up to five dimensions. We focus on two approaches: the Time Deep Gradient Flow (TDGF) method and the Deep Galerkin Method (DGM). We extend the TDGF method to handle the free-boundary partial differential equation inherent in American options. We carefully design the sampling strategy during training to enhance performance. Both TDGF and DGM achieve high accuracy while outperforming conventional Monte Carlo methods in terms of computational speed. In particular, TDGF tends to be faster during training than DGM.

• The paper introduces the Time Deep Gradient Flow (TDGF) method, formulating American option pricing as an energy minimization problem solved via neural networks.
• TDGF employs stratified sampling and a neural network with gated, residual layers to accurately approximate the free-boundary PDE in high dimensions.
• Numerical results under Black–Scholes and Heston models show TDGF’s scalability, improved convergence, and potential for real-time financial application.

Time Deep Gradient Flow Method for Pricing American Options

Problem Formulation and Theoretical Framework

The paper addresses the high-dimensional pricing of American put options under both the Black–Scholes and Heston models, focusing on the computational challenges posed by the early exercise feature and the curse of dimensionality. The American option pricing problem is formulated as a free-boundary PDE or, equivalently, a system of variational inequalities. The operator $\mathcal{A}$, which encodes the dynamics of the underlying assets, is derived for both the multidimensional Black–Scholes and Heston models, with explicit expressions for the drift and diffusion coefficients. The reformulation of the PDE as an energy minimization problem is central to the Time Deep Gradient Flow (TDGF) approach, enabling the use of neural networks for efficient approximation.

Time Deep Gradient Flow Methodology

The TDGF method discretizes the time interval $[0,T]$ into $K$ steps and, at each step, solves a variational problem by minimizing a cost functional that encodes the PDE dynamics. The solution at each time step is approximated by a neural network $f^k(\mathbf{x}; \theta)$, with the cost functional incorporating both the temporal difference and the spatial PDE terms. The minimization is performed using stochastic gradient descent, with the Adam optimizer and a carefully chosen learning rate.

A key innovation is the restriction of training to the region where the continuation value is positive, i.e., where the neural network output exceeds the payoff. This leverages the structure of the American option PDE, focusing computational effort on the relevant domain and improving efficiency.

Neural Network Architecture

The neural network architecture for TDGF closely follows the Deep Galerkin Method (DGM) design, employing gated layers and skip connections to facilitate the learning of complex solution manifolds. The network is structured as follows:

• Input layer processes the state variables (asset prices and, for Heston, volatilities).
• Multiple hidden layers (3 layers, 50 neurons each) with hyperbolic tangent activations.
• Gated and residual connections to enhance gradient flow and expressivity.
• Output layer adds the intrinsic value (payoff) to the learned continuation value, with a softplus activation to enforce the no-arbitrage lower bound.

This architecture ensures that the network output always satisfies $u \geq \Psi$, embedding the free-boundary constraint directly into the model.

Sampling Strategies for High-Dimensional Domains

Uniform sampling in high dimensions leads to poor coverage of the domain, especially near the boundaries where the continuation value is most sensitive. The paper introduces a box-based stratified sampling scheme, partitioning the domain into multiple boxes and sampling uniformly within each. This approach ensures adequate representation across the range of moneyness values, as illustrated in the following figures.

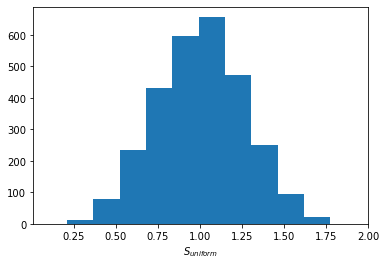
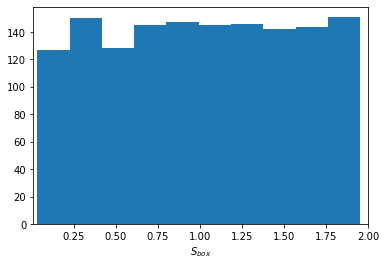
Figure 1: Uniform sampling in five dimensions leads to poor coverage at the domain edges, resulting in inadequate learning of the option value in these regions.

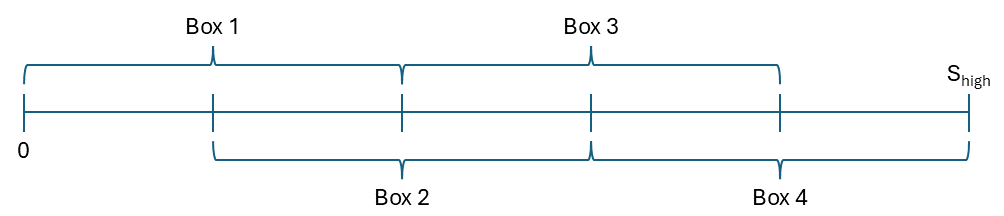
Figure 2: Box-based sampling with four boxes per dimension provides more uniform coverage across the moneyness domain, improving learning stability and accuracy.

This stratified sampling is used for initial training, while uniform sampling is employed during time-stepping, focusing on regions where the continuation value is positive.

Numerical Results: Accuracy and Efficiency

The TDGF and DGM methods are benchmarked against the Longstaff–Schwartz Monte Carlo approach across two- and five-dimensional Black–Scholes and Heston models. The primary metric is the difference between the option price and the payoff (i.e., the continuation value) as a function of moneyness, evaluated at multiple times to maturity.

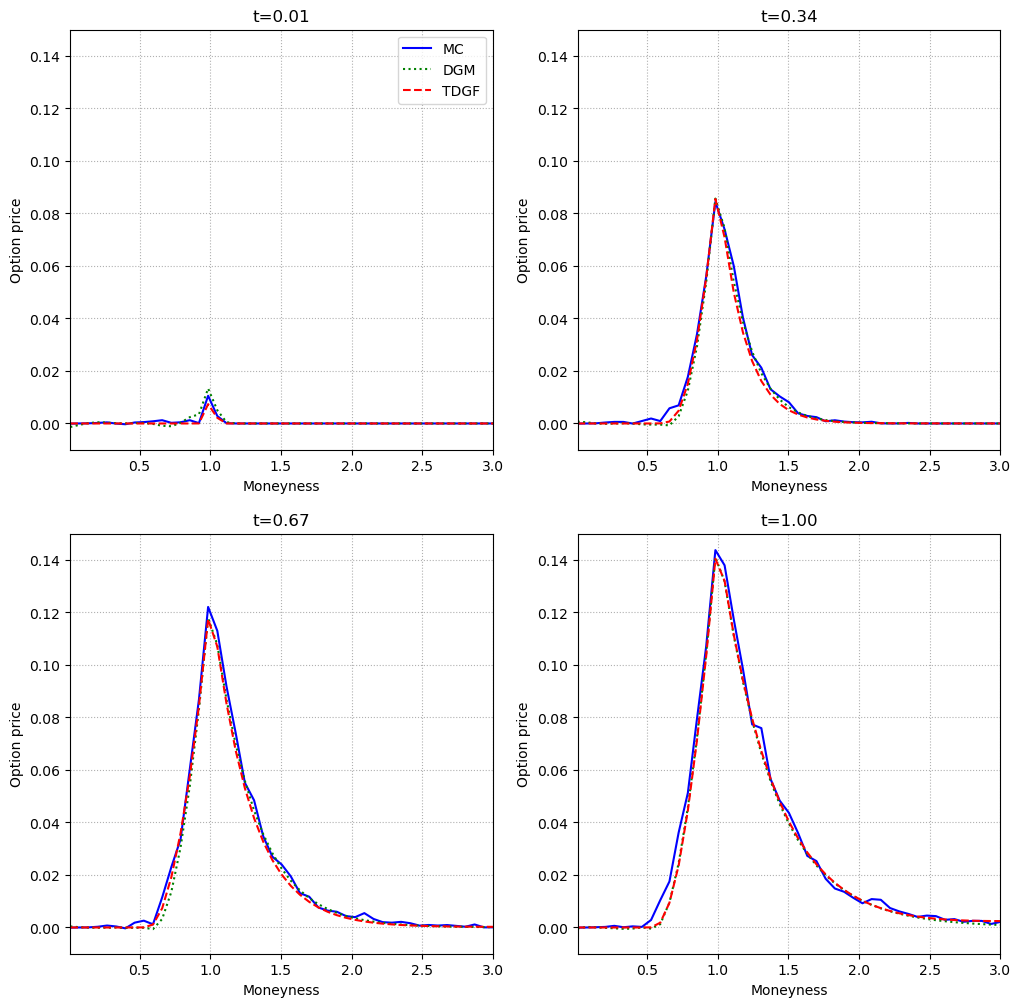
Figure 3: In the two-dimensional Black–Scholes model, TDGF and DGM closely match the Monte Carlo reference across all moneyness values and times to maturity.

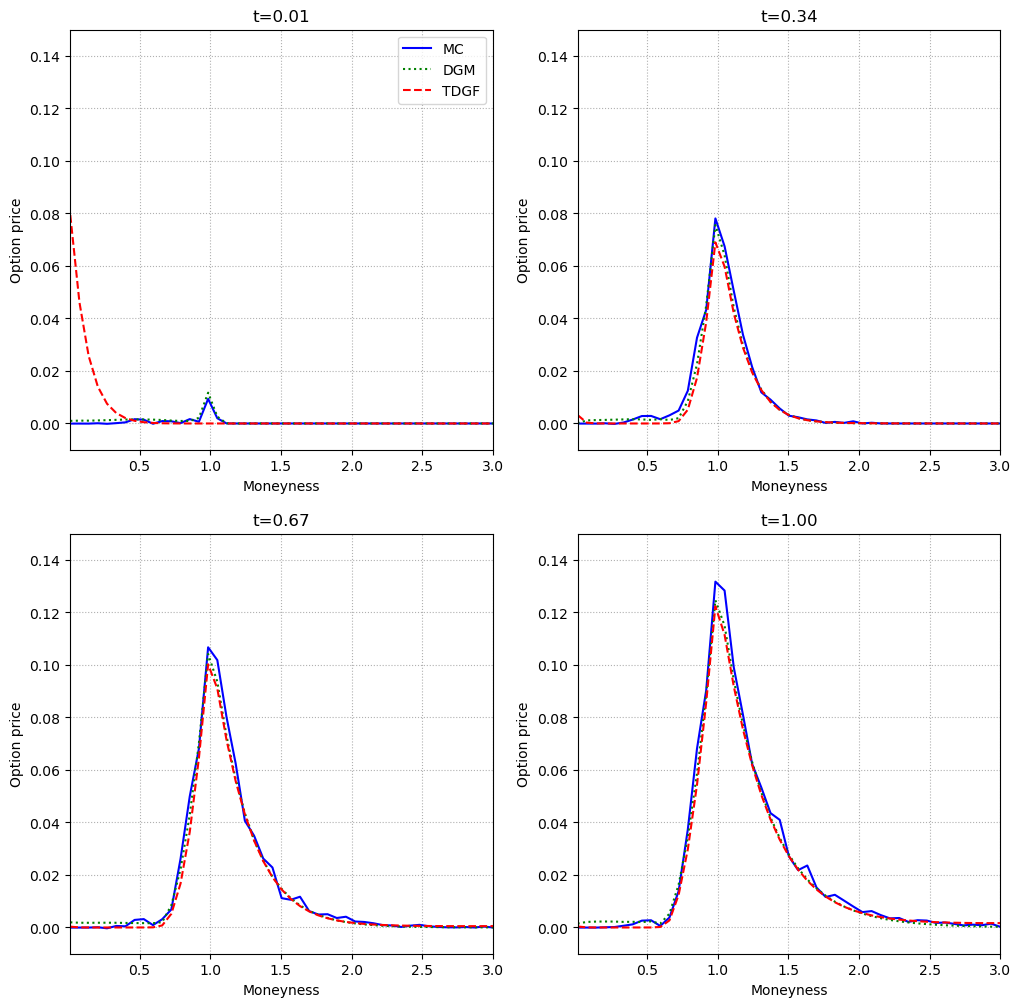
Figure 4: In the five-dimensional Black–Scholes model, both neural network methods maintain high accuracy, with negligible deviation from the Monte Carlo baseline.

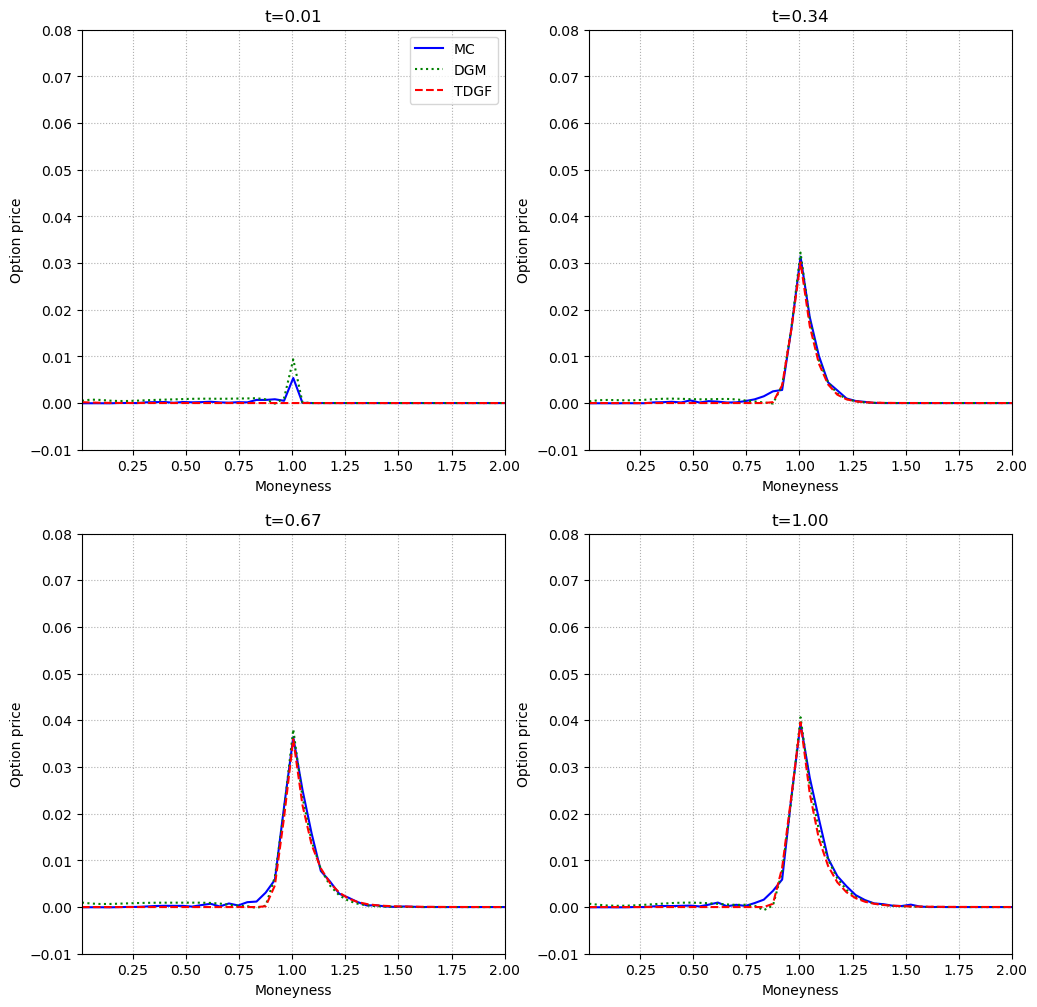
Figure 5: In the two-dimensional Heston model, TDGF and DGM again align with Monte Carlo, demonstrating robustness to stochastic volatility.

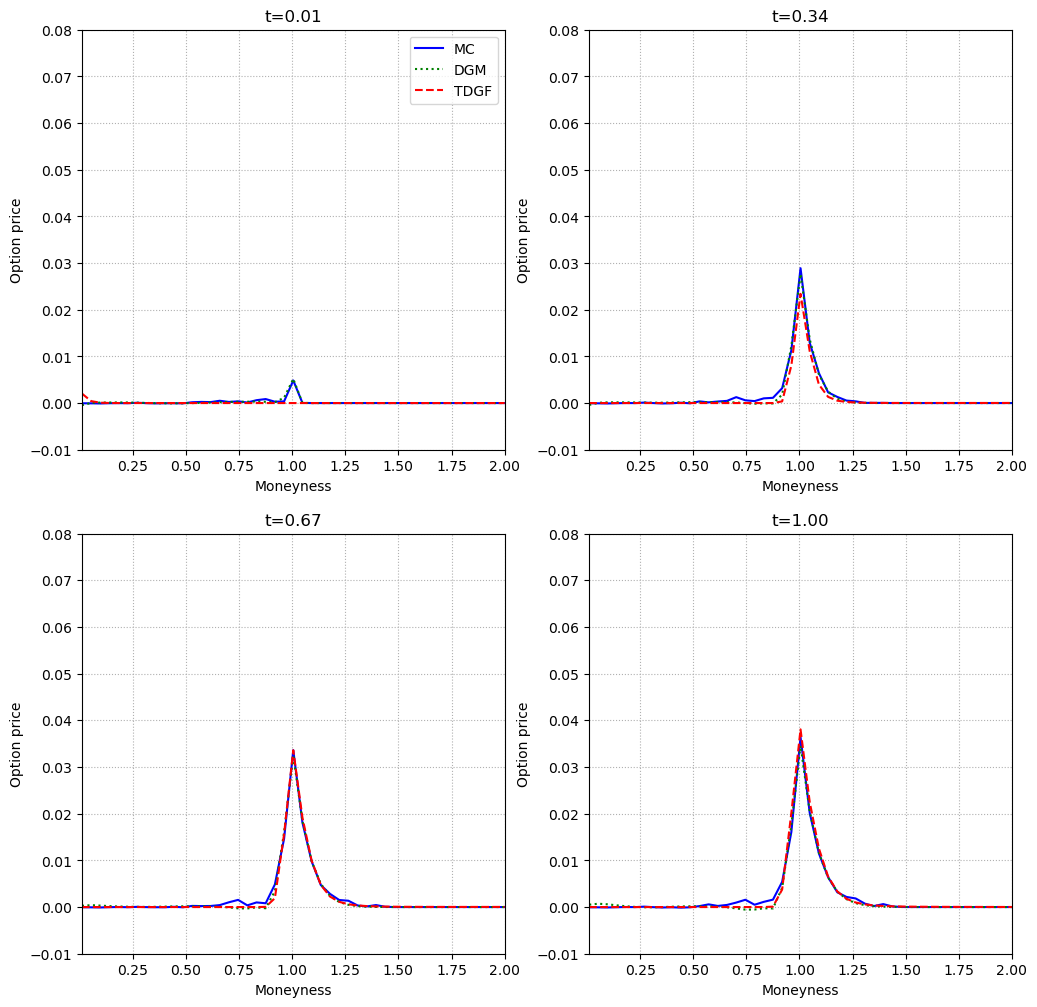
Figure 6: In the five-dimensional Heston model, the neural network methods remain accurate, even as the continuation value vanishes for high moneyness.

Across all settings, both TDGF and DGM achieve high accuracy, with the TDGF method exhibiting faster convergence and reduced training time. The computational time for inference is orders of magnitude lower than Monte Carlo, making these methods suitable for real-time or large-scale applications.

Practical Implications and Limitations

The extension of TDGF to free-boundary problems enables efficient pricing of high-dimensional American options, a task intractable for traditional grid-based PDE solvers. The method's scalability and speed make it attractive for risk management, portfolio optimization, and real-time pricing in multi-asset markets.

However, the approach relies on careful sampling and network architecture design. The accuracy of the method may degrade for extremely high dimensions or in the presence of path-dependent features not captured by the current formulation. The method also assumes access to sufficient computational resources (e.g., GPUs) for training.

Future Directions

Potential avenues for further research include:

• Extension to path-dependent and exotic options, requiring more sophisticated network architectures or recurrent structures.
• Adaptive sampling strategies that dynamically focus on regions of high error or sensitivity.
• Integration with uncertainty quantification techniques to provide confidence intervals on the predicted prices.
• Application to other classes of free-boundary PDEs in finance and beyond.

Conclusion

The paper demonstrates that the Time Deep Gradient Flow method, when extended to free-boundary PDEs, provides an efficient and accurate framework for pricing high-dimensional American options under both Black–Scholes and Heston models. The combination of energy-based time-stepping, neural network approximation, and stratified sampling yields significant improvements in computational speed and scalability over traditional Monte Carlo and PDE methods. The results suggest that TDGF is a viable tool for practical deployment in high-dimensional financial engineering tasks, with potential for further generalization and application.