SplitMeanFlow: Interval Splitting Consistency in Few-Step Generative Modeling (2507.16884v1)

Abstract: Generative models like Flow Matching have achieved state-of-the-art performance but are often hindered by a computationally expensive iterative sampling process. To address this, recent work has focused on few-step or one-step generation by learning the average velocity field, which directly maps noise to data. MeanFlow, a leading method in this area, learns this field by enforcing a differential identity that connects the average and instantaneous velocities. In this work, we argue that this differential formulation is a limiting special case of a more fundamental principle. We return to the first principles of average velocity and leverage the additivity property of definite integrals. This leads us to derive a novel, purely algebraic identity we term Interval Splitting Consistency. This identity establishes a self-referential relationship for the average velocity field across different time intervals without resorting to any differential operators. Based on this principle, we introduce SplitMeanFlow, a new training framework that enforces this algebraic consistency directly as a learning objective. We formally prove that the differential identity at the core of MeanFlow is recovered by taking the limit of our algebraic consistency as the interval split becomes infinitesimal. This establishes SplitMeanFlow as a direct and more general foundation for learning average velocity fields. From a practical standpoint, our algebraic approach is significantly more efficient, as it eliminates the need for JVP computations, resulting in simpler implementation, more stable training, and broader hardware compatibility. One-step and two-step SplitMeanFlow models have been successfully deployed in large-scale speech synthesis products (such as Doubao), achieving speedups of 20x.

• The paper introduces an algebraic interval splitting consistency identity that generalizes MeanFlow for efficient few-step generative modeling.
• It presents a hardware-friendly training algorithm that bypasses complex Jacobian-vector product computations, ensuring rapid and stable model updates.
• Empirical results in audio generation show that 1-step generation achieves parity with 10-step methods, confirming both efficiency and high-fidelity outputs.

SplitMeanFlow: Interval Splitting Consistency in Few-Step Generative Modeling

Motivation and Context

The computational inefficiency of iterative sampling in diffusion and flow-based generative models has motivated the development of few-step and one-step generative frameworks. While Flow Matching and its variants have achieved strong sample quality, their reliance on modeling instantaneous velocity fields and multi-step ODE integration remains a bottleneck for real-time and resource-constrained applications. MeanFlow advanced the field by proposing to learn the average velocity field, enabling direct mapping from noise to data in a single or few steps. However, MeanFlow's reliance on a differential identity introduces both theoretical and practical limitations, particularly due to the need for Jacobian-vector product (JVP) computations.

Algebraic Interval Splitting Consistency

SplitMeanFlow introduces a principled algebraic approach to learning the average velocity field for generative modeling. The core insight is to leverage the additivity property of definite integrals, leading to the Interval Splitting Consistency identity:

$$(t-r)u(z_t, r, t) = (s-r)u(z_s, r, s) + (t-s)u(z_t, s, t)$$

where $u(z_t, r, t)$ is the average velocity field over $[r, t]$, and $z_t$ is the flow path at time $t$. This identity holds for any $r \leq s \leq t$ and is derived directly from the integral definition of average velocity, bypassing the need for differential operators.

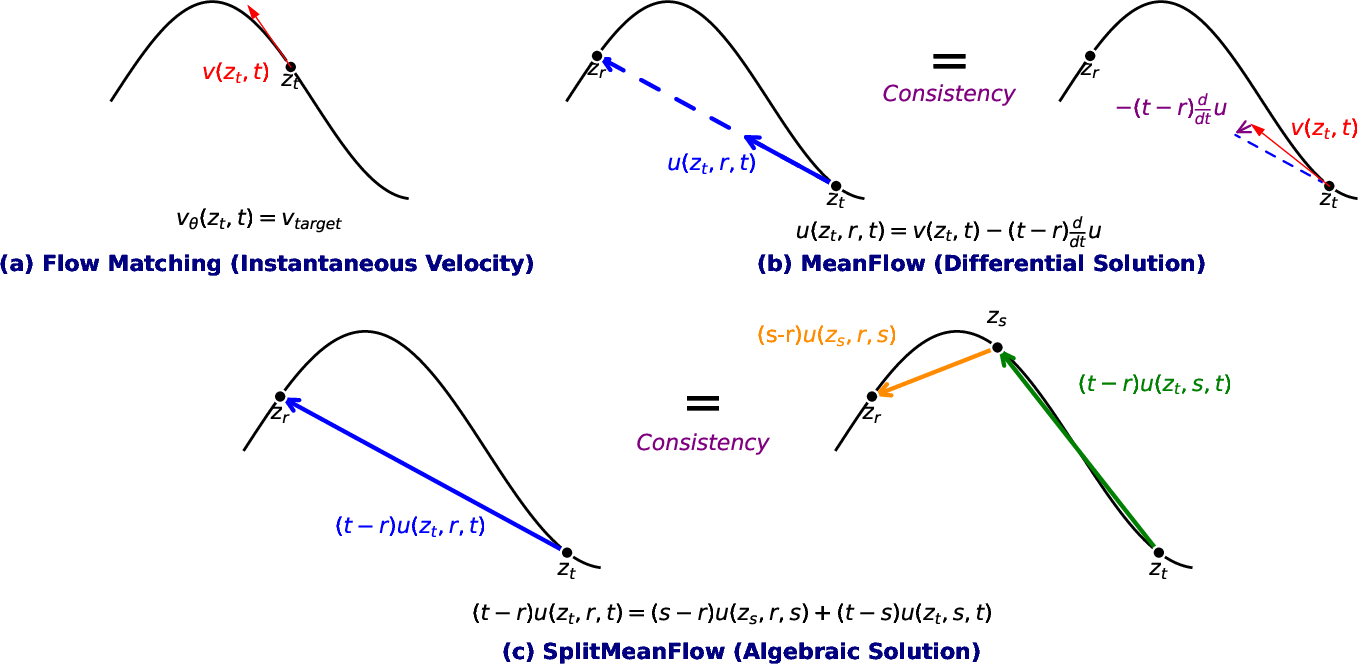
Figure 1: Conceptual comparison of generative flow methods, highlighting the transition from instantaneous velocity (Flow Matching) to average velocity (MeanFlow, SplitMeanFlow) and the algebraic self-consistency of SplitMeanFlow.

This algebraic formulation generalizes the MeanFlow differential identity, which is recovered as a limiting case when $s \to t$. The approach is thus both more fundamental and more flexible, providing a self-referential constraint that can be enforced at arbitrary interval splits.

Training Algorithm and Implementation

The SplitMeanFlow training procedure enforces the Interval Splitting Consistency as a self-supervised objective. The key steps are:

1. Sample time points $r, t$ with $0 \leq r < t \leq 1$, and a random $\lambda \sim \mathcal{U}(0,1)$; set $s = (1-\lambda)t + \lambda r$.
2. Sample prior $\epsilon \sim \mathcal{N}(0, I)$.
3. Construct flow path $z_t = (1-t)x + t\epsilon$.
4. Compute $u_2 = u_\theta(z_t, s, t)$.
5. Compute intermediate point $z_s = z_t - (t-s)u_2$.
6. Compute $u_1 = u_\theta(z_s, r, s)$.
7. Form target $target = (1-\lambda)u_1 + \lambda u_2$.
8. Loss: $$\mathcal{L} = \|u_\theta(z_t, r, t) - \text{sg}(target)\|$$ (where $\text{sg}$ is stop-gradient).

This procedure requires only standard forward and backward passes, with no JVPs or higher-order derivatives, resulting in a simple and hardware-friendly implementation.

Pseudocode

def splitmeanflow_step(u_theta, x_batch, optimizer): r, t = sample_time_points() lambda_ = np.random.uniform(0, 1) s = (1 - lambda_) * t + lambda_ * r epsilon = np.random.normal(size=x_batch.shape) z_t = (1 - t) * x_batch + t * epsilon u2 = u_theta(z_t, s, t) z_s = z_t - (t - s) * u2 u1 = u_theta(z_s, r, s) target = (1 - lambda_) * u1 + lambda_ * u2 loss = ((u_theta(z_t, r, t) - target.detach()) ** 2).mean() optimizer.zero_grad() loss.backward() optimizer.step()

Boundary Conditions and Distillation

To avoid degenerate solutions, the model is anchored by enforcing $u(z_t, t, t) = v(z_t, t)$ at the boundary, where $v$ is the instantaneous velocity from a pretrained teacher model. In practice, a two-stage training regime is used: first, a standard flow matching model is trained as the teacher; then, SplitMeanFlow is distilled from this teacher, mixing the boundary condition and interval splitting losses.

Theoretical and Practical Advantages

Theoretical Generality

The algebraic identity of SplitMeanFlow subsumes the MeanFlow differential identity as a special case. In the limit $s \to t$, the difference quotient on the left-hand side becomes a derivative, and the right-hand side converges to the instantaneous velocity, exactly recovering the MeanFlow update. This demonstrates that SplitMeanFlow is a strict generalization, providing a more robust and theoretically grounded framework for learning average velocity fields.

Computational Efficiency

SplitMeanFlow eliminates the need for JVPs, which are required in MeanFlow to compute $\frac{d}{dt}u$. This results in:

• Simpler implementation: Only standard forward and backward passes are needed.
• Improved stability: Avoids numerical issues associated with higher-order derivatives.
• Broader hardware compatibility: No reliance on JVP support in accelerators or frameworks.
• Faster training: Reduced computational overhead per iteration.

Empirical Results

SplitMeanFlow was evaluated on large-scale audio generation tasks using the Seed-TTS framework. Key findings include:

• 2-step SplitMeanFlow matches or slightly exceeds the 10-step Flow Matching baseline in speaker similarity (SIM: 0.789 vs. 0.787) and achieves nearly identical word error rate (WER: 0.0561 vs. 0.0551) and subjective CMOS scores.
• 1-step SplitMeanFlow achieves parity with 10-step Flow Matching in in-context learning tasks, with identical WER (0.0286) and negligible difference in SIM (0.685 vs. 0.686), and a neutral CMOS score, indicating no perceptual degradation.
• No need for Classifier-Free Guidance (CFG), further reducing inference complexity.

These results demonstrate that SplitMeanFlow enables high-fidelity, few-step, and even one-step generation with minimal quality loss and substantial computational savings.

Implications and Future Directions

SplitMeanFlow's algebraic approach to learning average velocity fields provides a new foundation for efficient generative modeling. Its theoretical generality and practical simplicity make it well-suited for deployment in latency-sensitive and resource-constrained environments, as evidenced by its industrial adoption.

Potential future directions include:

• Extension to other modalities: Application to image, video, and multimodal generative tasks.
• Integration with advanced architectures: Combining with transformer-based or hierarchical models for further gains.
• Exploration of alternative self-supervised consistency objectives: Generalizing the algebraic approach to other forms of generative modeling and distillation.
• Theoretical analysis of convergence and expressivity: Formal paper of the conditions under which algebraic self-consistency leads to optimal generative performance.

Conclusion

SplitMeanFlow establishes a principled, algebraic framework for few-step generative modeling by enforcing interval splitting consistency. It generalizes and improves upon prior differential approaches, offering both theoretical robustness and practical efficiency. The method achieves state-of-the-art performance in one-step and few-step generation tasks, with strong empirical results and demonstrated industrial impact. This work opens new avenues for efficient, high-quality generative modeling across domains.