The gravitational potential of spiral perturbations. I the 2D (razor-thin) case (2507.16615v1)

Abstract: I develop an efficient numerical method to obtain the gravitational potential of razor-thin spiral perturbations and use it to assess the standard tight-winding (or WKB) approximation, which is found reasonably accurate for pitch angles $\alpha\lesssim 20\deg$. I extend Kalnajs' (1971)' potential-density pairs to logarithmic spirals with arbitrary power-law amplitude. Approximating a spiral locally by one of these models provides a second-order tight-winding approximation that predicts the phase offset between spiral potential and density, the resulting radially increasing pitch of the potential, and the non-local outward angular-momentum transport by gravitational torques. Beyond the inner and outer edge of a spiral with m arms, its potential is not winding ($\alpha=90\deg$), decays like $R^m$ and $R^{-1-m}$, respectively, and cannot be predicted by a local approximation.

• The paper presents a robust numerical method to compute gravitational potentials of arbitrary spiral perturbations in razor-thin discs, improving upon traditional WKB approaches.
• The paper introduces a second-order tight-winding approximation that accurately captures both amplitude and phase offsets, enhancing predictions of gravitational torques in galactic models.
• The method generalizes Kalnajs potential-density pairs and quantifies the limitations of the WKB approximation, offering actionable insights for realistic spiral structure modeling.

The Gravitational Potential of Spiral Perturbations in Razor-Thin Discs

Introduction and Motivation

The gravitational potential generated by spiral density perturbations in razor-thin galactic discs is a central problem in galactic dynamics, underpinning models of spiral structure, secular evolution, and radial migration. While the tight-winding (WKB) approximation is widely used to estimate the potential of spiral arms, its accuracy and limitations, especially for realistic spiral morphologies, have not been systematically quantified. This work develops an efficient numerical method for computing the gravitational potential of arbitrary razor-thin spiral perturbations, rigorously assesses the WKB approximation, and introduces a novel, more accurate second-order tight-winding approximation. The paper also generalizes the classic Kalnajs (1971) potential-density pairs to logarithmic spirals with arbitrary power-law amplitude, providing new analytic tools for disc dynamics.

Mathematical Framework and Numerical Methods

The analysis is restricted to two-dimensional (razor-thin) discs, where the surface density $\Sigma(\vec{R})$ is related to the gravitational potential $\Psi(\vec{R})$ in the midplane via the Poisson integral: $$\Psi(\vec{R}) = -G \iint \frac{\Sigma(\vec{R}')\,d^2\vec{R}'}{|\vec{R} - \vec{R}'|}$$ and, conversely, the surface density can be recovered from the potential using: $$\Sigma(\vec{R}) = \frac{1}{4\pi^2 G} \iint \frac{\nabla^2 \Psi(\vec{R}')\,d^2\vec{R}'}{|\vec{R} - \vec{R}'|}$$ The paper implements a highly efficient numerical solver for these relations, leveraging azimuthal Fourier decomposition and fast evaluation of Laplace coefficients (see Appendix for algorithmic details).

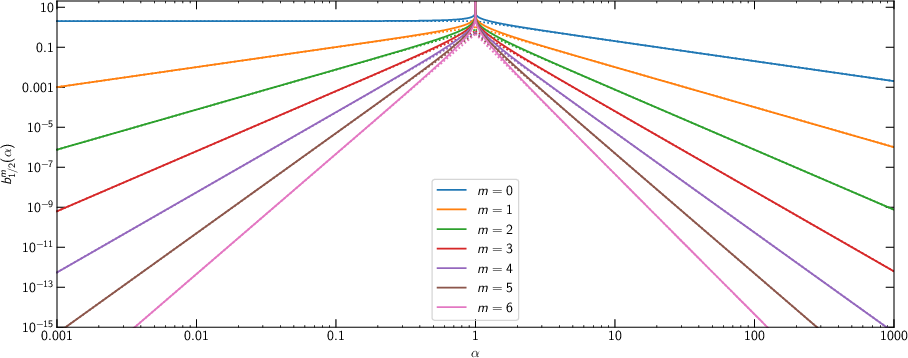
Figure 1: The Laplace coefficients $b_{1/2}$, essential for the efficient computation of the Poisson integral in azimuthal Fourier space.

Spiral Models and the Tight-Winding Approximation

Spiral perturbations are modeled as azimuthal Fourier components with amplitude and phase functions: $$\Sigma(\vec{R}) = S_m(R) \exp\left[i m (\phi - \psi_s(R))\right]$$

$$\Psi(\vec{R}) = -P_m(R) \exp\left[i m (\phi - \psi_p(R))\right]$$

The pitch angle $\alpha$ is related to the radial derivative of the phase. For logarithmic spirals, $\psi(R) = \lambda \ln(R/R_0)$, yielding constant pitch angle.

The standard tight-winding (WKB) approximation assumes the local spiral can be treated as a plane wave, leading to: $$\Psi(\vec{R}) \approx -\frac{2\pi G}{k(R)} \Sigma(\vec{R})$$ with $k(R)$ the local wavenumber. Two forms are considered:

• $k(R) = m/(R \tan\alpha)$ (traditional)
• $k(R) = m/(R \sin\alpha)$ (more accurate, includes azimuthal wavenumber)

The first-order WKB approximation predicts no phase offset between potential and density, while the second-order (Shu 1970) approximation introduces a phase shift but is not directly invertible.

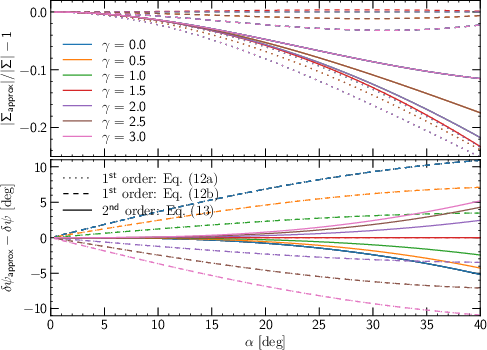
Figure 2: Assessment of the tight-winding (WKB) approximation for scale-invariant logarithmic spirals, showing amplitude and phase errors as a function of pitch angle.

Generalization of Kalnajs Spirals and Second-Order Approximation

The paper extends Kalnajs' (1971) analytic potential-density pairs to logarithmic spirals with arbitrary power-law amplitude, $\Sigma \propto R^{-\gamma}$. The potential in the midplane is: $$\Psi(\vec{R}) = -2\pi G K_m(\zeta) R \Sigma(\vec{R})$$ where $K_m(\zeta)$ is a complex function of the spiral parameters, with its modulus and argument controlling amplitude and phase offset, respectively.

A key result is the derivation of a second-order tight-winding approximation by locally matching the spiral to a scale-invariant model: $$\Psi(\vec{R}) \approx -2\pi G \frac{\sin\alpha}{m} \left[1 + i\sigma \frac{\sin 2\alpha}{2m} (\gamma - 3/2)\right] R \Sigma(\vec{R})$$ This form captures both amplitude corrections and the phase offset between potential and density, which is crucial for modeling angular momentum transport.

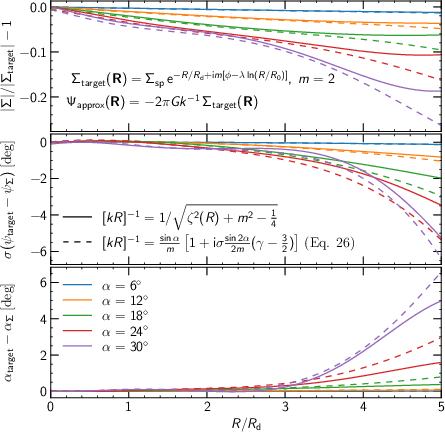
Figure 3: Comparison of the first-order (left) and novel second-order (right) tight-winding approximations for the gravitational potential of a target spiral density.

Numerical Assessment and Application to Realistic Spirals

The numerical method is applied to spirals with exponential amplitude profiles, as observed in real galaxies. The first-order WKB approximation with $k(R) = m/(R \sin\alpha)$ provides reasonable amplitude estimates for $\alpha \lesssim 20^\circ$, but fails to capture the phase offset and the radially increasing pitch of the potential. The second-order approximation significantly improves the phase prediction.

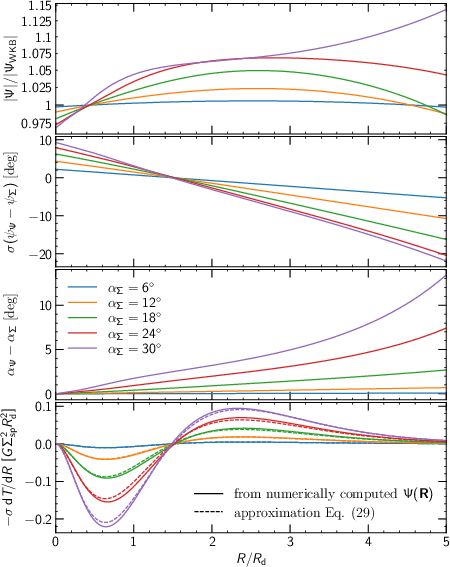
Figure 4: Properties of a spiral with exponential amplitude, showing amplitude ratio, phase offset, pitch angle deviation, and torque per annulus.

At large radii or for spirals with sharp radial truncation, all local approximations fail, and the potential is dominated by the non-local field from the inner disc, decaying as $R^{-1-m}$.

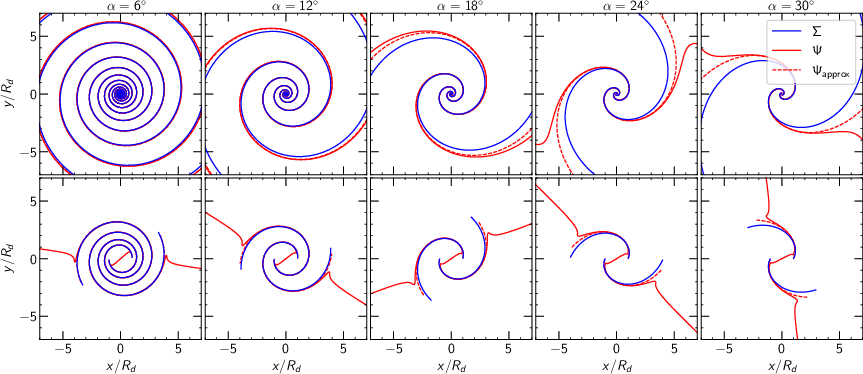
Figure 5: Crest lines of density (blue) and potential (red) for logarithmic $m=2$ spirals, illustrating the phase offset and pitch angle evolution for unlimited and truncated spirals.

Gravitational Torques and Angular Momentum Transport

The phase offset between potential and density leads to a net gravitational torque, which is second-order in both amplitude and pitch angle. For trailing spirals, the torque is negative at small radii and positive at large radii, implying outward angular momentum transport. The paper derives a simple analytic approximation for the local mean torque density: $$\langle \tau_\phi \rangle \approx -\frac{\sigma\pi}{2m} G R S_m^2 \sin\alpha \sin 2\alpha (\gamma - 3/2)$$ This result is robust for a wide range of spiral models and is validated against numerical calculations.

Implications for Spiral Modeling and Galactic Dynamics

The paper demonstrates that many commonly used analytic spiral potentials, based on the first-order WKB approximation, can yield density patterns that deviate significantly from the intended target, especially when the spiral is radially limited or the pitch angle is large. This can lead to unphysical results in dynamical models, such as incorrect radial migration rates or spurious bar-like features at spiral edges.

The second-order approximation provides a practical improvement, but for accurate modeling of realistic, radially truncated spirals, direct numerical computation of the potential is necessary. The provided numerical method is efficient and suitable for integration into galactic modeling codes.

Performance, Implementation, and Scaling

The numerical solver is implemented in both C++ and Python, with performance dominated by the evaluation of Laplace coefficients and the radial convolution integrals. The method scales linearly with the number of radial grid points and is highly parallelizable over azimuthal modes. For typical disc models with $N_R \sim 10^3$ and $m \leq 6$, the potential can be computed in seconds on modern CPUs.

Limitations and Future Directions

The analysis is restricted to razor-thin discs and the midplane potential. For discs with significant vertical thickness, the potential is overestimated by a factor $(1 + h_z k)^{-1}$, where $h_z$ is the scale height and $k$ the local wavenumber. Extension to fully three-dimensional models is identified as a necessary future step.

Conclusion

This work provides a comprehensive framework for computing and understanding the gravitational potential of spiral perturbations in razor-thin discs. The main contributions are:

• A robust numerical method for arbitrary spiral patterns.
• A systematic assessment of the WKB approximation, quantifying its domain of validity.
• A novel, second-order tight-winding approximation that accurately predicts amplitude and phase offset.
• Generalization of Kalnajs' analytic spirals to arbitrary power-law amplitudes.
• Analytic and numerical quantification of gravitational torques and their role in angular momentum transport.

These results have direct implications for the construction of realistic galactic models, the interpretation of spiral-driven secular evolution, and the design of future $N$-body and hydrodynamic simulations.

Figure 6: Accuracy of the asymptotic approximation for $K_m(\zeta)$, demonstrating the validity of the analytic approach for a wide range of spiral parameters.

References to Figures

• Figure 6: Validates the analytic approximation for $K_m(\zeta)$.
• Figure 2: Quantifies WKB approximation errors for scale-invariant spirals.
• Figure 3: Compares first- and second-order tight-winding approximations.
• Figure 4: Shows numerical results for exponential spirals.
• Figure 5: Visualizes crest lines and phase offsets for various spiral models.
• Figure 1: Illustrates Laplace coefficients used in the numerical method.

Outlook

The methods and results presented here set a new standard for the modeling of spiral structure in galactic discs. The numerical tools and analytic approximations are immediately applicable to studies of disc stability, secular evolution, and the interpretation of stellar kinematic data. Future work will extend these techniques to three-dimensional discs and time-dependent spiral patterns, further bridging the gap between analytic theory and realistic galactic modeling.