Diffusion Beats Autoregressive in Data-Constrained Settings (2507.15857v3)

Abstract: Autoregressive (AR) models have long dominated the landscape of LLMs, driving progress across a wide range of tasks. Recently, diffusion-based LLMs have emerged as a promising alternative, though their advantages over AR models remain underexplored. In this paper, we systematically study masked diffusion models in data-constrained settings-where training involves repeated passes over limited data-and find that they significantly outperform AR models when compute is abundant but data is scarce. Diffusion models make better use of repeated data, achieving lower validation loss and superior downstream performance. We interpret this advantage as implicit data augmentation: masked diffusion exposes the model to a diverse distribution of token orderings and prediction tasks, unlike AR's fixed left-to-right factorization. We find new scaling laws for diffusion models and derive a closed-form expression for the critical compute threshold at which diffusion begins to outperform AR. These results suggest that when data, not compute, is the bottleneck, diffusion models offer a compelling alternative to the standard AR paradigm. Our code is available at: https://diffusion-scaling.github.io.

• The paper demonstrates that masked diffusion models can outperform autoregressive models in scenarios where data is limited but compute is abundant.
• It reveals that diffusion models benefit significantly from repeated data, effectively utilizing many epochs compared to AR models.
• The study introduces scaling laws that predict when diffusion models become advantageous based on unique token counts and compute budgets.

Diffusion vs. Autoregressive Models in Data-Constrained Scenarios

The paper "Diffusion Beats Autoregressive in Data-Constrained Settings" (2507.15857) addresses the question of data efficiency in LLMs by comparing masked diffusion models with autoregressive (AR) models in scenarios where data is limited and compute is abundant. It challenges the conventional wisdom that AR models are always superior, particularly in light of potential data bottlenecks in the future. The paper reveals that diffusion models can outperform AR models when trained extensively on repeated data, offering a compelling alternative when data is the primary constraint.

Background and Motivation

The scaling of LLMs has traditionally relied on proportional increases in both compute and data. However, the availability of high-quality data is not keeping pace with compute advancements, potentially limiting future scaling. Moreover, in domains like robotics and healthcare, data scarcity is already a significant bottleneck. AR models have been the dominant paradigm in LLMs, but diffusion-based models have emerged as a promising alternative. While diffusion models have shown similar scaling behavior to AR models, their practical benefits have been limited due to their high compute requirements. Previous research indicates that diffusion models may require up to 16 times more compute than AR models to achieve comparable performance in single-epoch training regimes. The paper investigates whether this apparent inefficiency is due to a genuine need for more compute or simply a greater need for more data.

Methodology

The paper systematically compares masked diffusion models and AR models in data-constrained settings, where models are trained for multiple epochs on limited data. The authors train hundreds of models, varying model size, data quantity, and the number of training epochs. The paper keeps the architecture (GPT-2 style with RoPE) and data pipeline fixed across both model families, varying only the factorization of the joint distribution. AR models predict each token based on prior tokens in a left-to-right fashion, while diffusion models treat generation as iterative denoising, predicting masked tokens with bidirectional attention. The authors use the English C4 corpus, tokenized with the GPT-2 BPE vocabulary, and train models ranging from 7M to 2.5B parameters, following the Chinchilla scaling strategy.

(Figure 1)

Figure 1: Pareto frontier of validation loss versus training FLOPs for autoregressive (AR) and masked diffusion models under data-constrained settings.

To model the diminishing returns from repeated data, the authors adopt a scaling framework that incorporates an effective unique data size, $D'$, based on the idea that each additional epoch contributes less useful signal. The scaling law incorporates parameters such as $R_D^*$, which characterizes the number of epochs after which training more epochs results in significantly diminished returns.

Key Findings

The paper's findings challenge the conventional view of diffusion models as inherently less efficient:

1. Diffusion models surpass AR models given sufficient compute: AR models initially outperform diffusion models at low compute, but quickly saturate. Beyond a critical compute threshold, diffusion models continue improving and achieve better performance.
2. Diffusion models benefit far more from repeated data: Diffusion models can be trained on repeated data for up to 100 epochs, with repeated data almost as effective as fresh data. In contrast, AR models benefit from repeating the dataset up to approximately 4 epochs.
3. Diffusion models have a much higher effective epoch count: The paper estimates $R_D^* \approx 500$ for diffusion models, compared to $R_D^* \approx 15$ for AR models, indicating that diffusion models can benefit from repeated data over far more epochs without major degradation.
4. Critical compute point follows a power law with dataset size: The amount of compute required for diffusion models to outperform AR models scales as a power law with the number of unique tokens, yielding a closed-form expression for predicting when diffusion becomes the favorable modeling choice. Specifically, the critical compute, $C_{\mathrm{crit}(U)}$, scales with the number of unique tokens $U$ as $C_{\mathrm{crit}(U) \propto U^{2.174}}$.
5. Diffusion models yield better downstream performance: The best diffusion models trained in data-constrained settings consistently outperform the best AR models on a range of downstream language tasks.

Data-Constrained Scaling Laws

The authors fit scaling laws to both model families, varying the amount of unique data, model parameter count, and number of training epochs. The results show that diffusion models yield significantly higher $R^2$ values, reflecting a better overall fit, likely due to the absence of overfitting in diffusion models, even at high epoch counts. The extracted scaling parameters reveal a sharp contrast in data reuse half-lives, with diffusion models exhibiting an $R_D^*$ of 512.85, compared to just 31.93 for AR models. This indicates that diffusion models can extract more value from repeated data.

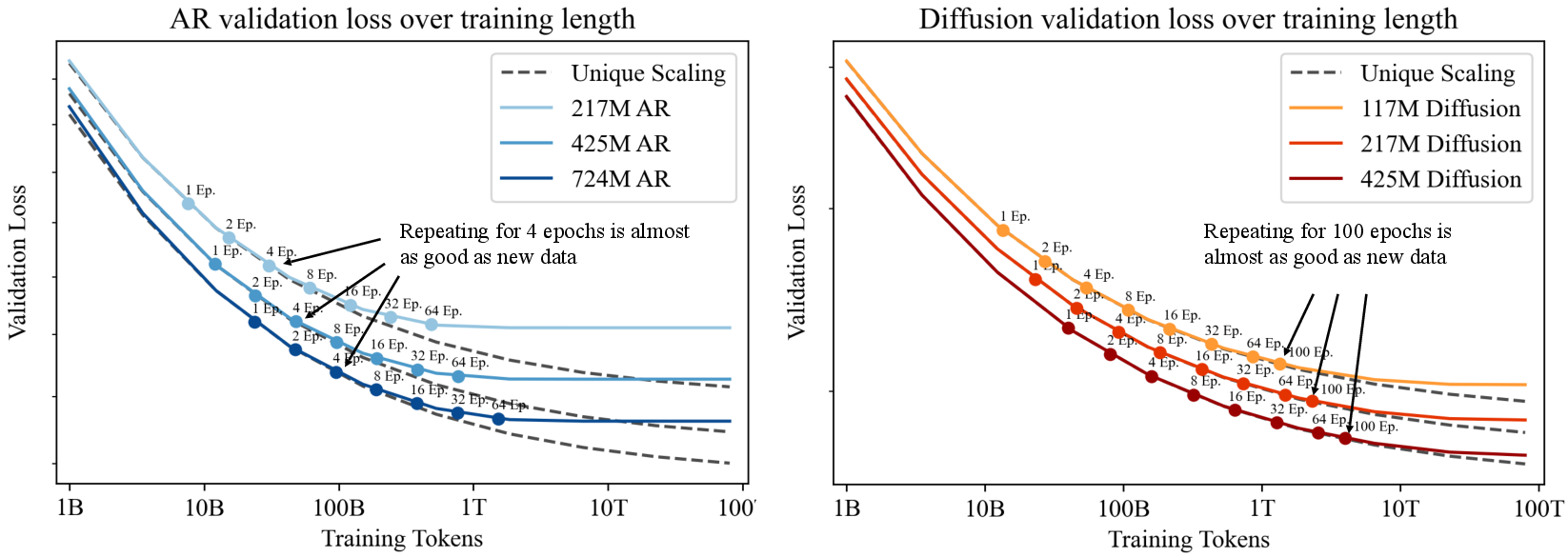
Figure 3: Predicted validation loss for AR models (left) and Diffusion models (right) under compute-optimal settings, extrapolated to larger compute budgets.

Implications and Discussion

The results suggest that the random factorizations inherent in the diffusion objective serve as a form of implicit data augmentation. Unlike AR models, which are trained on a single, fixed left-to-right ordering, masked diffusion models are exposed to a wide variety of token prediction tasks and orderings during training. This broader distribution over prediction tasks encourages better generalization and more effective use of each training example. The paper hypothesizes that AR models are more compute-efficient due to order specialization and stronger supervision per update.

Conclusion

The paper demonstrates that masked diffusion models can outperform AR models in data-constrained regimes, challenging the conventional belief that AR models are universally superior. The findings highlight diffusion models as a compelling alternative when data, not compute, is the primary bottleneck. For practitioners, the key takeaway is that AR models are preferable when compute is constrained, while diffusion models are more suitable when data is the limiting factor.