The Serial Scaling Hypothesis (2507.12549v1)

Abstract: While machine learning has advanced through massive parallelization, we identify a critical blind spot: some problems are fundamentally sequential. These "inherently serial" problems-from mathematical reasoning to physical simulations to sequential decision-making-require dependent computational steps that cannot be parallelized. Drawing from complexity theory, we formalize this distinction and demonstrate that current parallel-centric architectures face fundamental limitations on such tasks. We argue that recognizing the serial nature of computation holds profound implications on machine learning, model design, hardware development. As AI tackles increasingly complex reasoning, deliberately scaling serial computation-not just parallel computation-is essential for continued progress.

• The paper's main contribution is the argument for serial computation scaling in AI, challenging parallel-centric paradigms.
• It employs complexity theory to distinguish serial from parallel tasks, using examples like cellular automata and sequential decision processes.
• The findings imply that future model design, hardware, and evaluation should prioritize deep sequential processing for complex reasoning.

The Serial Scaling Hypothesis: Scaling Depth for AI Progress

The paper "The Serial Scaling Hypothesis" (2507.12549) challenges the prevailing focus on parallel computation in machine learning, arguing that progress in complex reasoning, planning, and system evolution necessitates scaling serial computation. The authors formalize this distinction using complexity theory and demonstrate limitations of parallel-centric architectures on inherently serial tasks, impacting model design, hardware development, and evaluation metrics.

Inherently Serial Problems

The authors define a problem as inherently serial if it does not belong to the complexity class $\mathsf{TC}$, meaning it cannot be efficiently solved by a polynomial-width, polylogarithmic-depth circuit with threshold gates. They posit that many real-world problems, particularly those involving complex reasoning, planning, or interacting systems, fall into this category. The paper highlights several examples:

• Cellular Automata (CA): Predicting the evolution of CA, especially Turing-complete variants like Rule 110, requires step-by-step computation due to the complex dependencies between cell states (Figure 1). Attempting to parallelize CA evolution leads to an exponential depth-width trade-off, making it computationally infeasible.

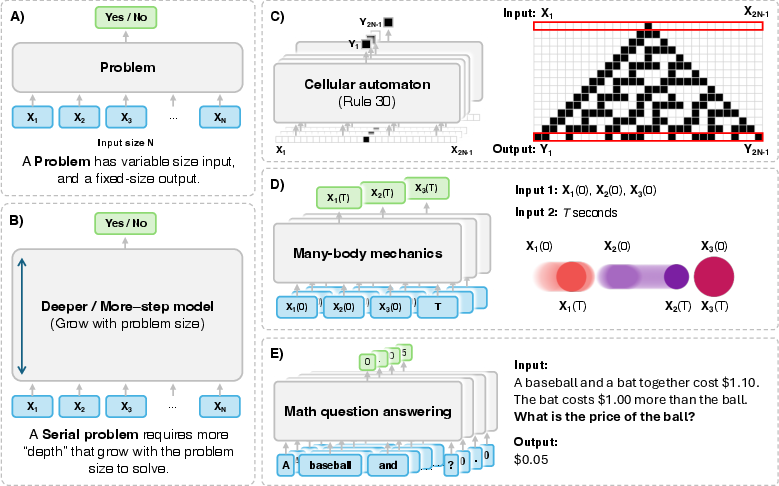
  Figure 1: (A) A decision problem has a variable-size input and a fixed-size output (e.g., yes''/no''). (B) A serial problem requires deeper or more steps as the problem size grows. Examples of serial problems are: (C) Cellular automaton: takes the initial state as input and outputs a discrete value of the row $N$ at cell $i$ for $i \in \{1, \dots, 2N-1\}$.

• Many-Body Mechanics: Simulating the motion of $N$ particles under Newtonian mechanics or hard collisions is inherently serial. Billiard-ball computers, which can simulate any Turing machine using particle collisions, exemplify this seriality. Parallel algorithms like Parareal may offer speedups for slowly changing ODEs, but fast-changing ODEs often require serial computation.
• Sequential Decision Problems: Finding the optimal policy in a Markov Decision Process (MDP) often necessitates accurate return estimation, which can be a serial bottleneck. While parallel computation can reduce variance in gradient estimation, it cannot replace the serial computation needed for accurate return estimation.
• Math Question Answering: Solving complex mathematical problems often requires step-by-step logical reasoning, making it inherently serial. Empirical evidence suggests that longer reasoning chains consistently outperform majority voting in math QA, emphasizing the importance of serial computation.

Limitations of Current ML Models

The paper argues that current machine learning models, particularly Transformers, SSMs, and diffusion models, often struggle with inherently serial problems due to their parallel-centric architectures. These models can be simulated by uniform threshold circuits of constant depth ($\mathsf{TC}^0$), limiting their ability to capture long-range dependencies that unfold over sequential steps.

Diffusion models, despite their iterative denoising process, are also shown to be limited to $\mathsf{TC}^0$ when using a fixed-depth $\mathsf{TC}^0$ backbone. This theoretical result suggests that diffusion models cannot provide a scalable means of increasing serial computation.

Implications for Future Research

The Serial Scaling Hypothesis has significant implications for future research in machine learning:

• Model Design: Future models should incorporate recurrent structures and mechanisms that allow for deeper or more sequential computation to address inherently serial problems effectively. However, this introduces trainability challenges such as increased gradient variance and model L-Lipschitzness.
• Hardware: Hardware development should prioritize low-latency, sequential processing capabilities to support serial computation. This may involve revisiting CPU designs or specialized processors that tightly integrate memory and compute.
• Evaluation: Evaluation metrics should distinguish between serial compute and total compute to better understand the computational requirements of different tasks and models.

Addressing Misconceptions

The paper addresses potential misconceptions regarding the Serial Scaling Hypothesis, particularly concerning the distinction between architecture and inference methods. While architectures like Transformers are inherently parallel, inference methods like Chain of Thought can introduce serial computation. The authors also clarify that SSMs, despite their recurrent nature, are designed for parallelizability and lack the inherent seriality of RNNs.

Conclusion

"The Serial Scaling Hypothesis" (2507.12549) provides a compelling argument for the importance of serial computation in machine learning. By formalizing the distinction between parallel and serial problems, the authors highlight the limitations of current parallel-centric architectures and offer valuable insights for future model design, hardware development, and evaluation metrics. The emphasis on the need for deeper, more sequential models opens new avenues for research in AI, potentially leading to more robust and generalizable solutions for complex real-world problems.