Massive Values in Self-Attention Modules are the Key to Contextual Knowledge Understanding (2502.01563v4)

Abstract: LLMs have achieved remarkable success in contextual knowledge understanding. In this paper, we show that these concentrated massive values consistently emerge in specific regions of attention queries (Q) and keys (K) while not having such patterns in values (V) in various modern transformer-based LLMs (Q, K, and V mean the representations output by the query, key, and value layers respectively). Through extensive experiments, we further demonstrate that these massive values play a critical role in interpreting contextual knowledge (knowledge obtained from the current context window) rather than in retrieving parametric knowledge stored within the model's parameters. Our further investigation of quantization strategies reveals that ignoring these massive values leads to a pronounced drop in performance on tasks requiring rich contextual understanding, aligning with our analysis. Finally, we trace the emergence of concentrated massive values and find that such concentration is caused by Rotary Positional Encoding (RoPE), which has appeared since the first layers. These findings shed new light on how Q and K operate in LLMs and offer practical insights for model design and optimization. The Code is Available at https://github.com/MingyuJ666/Rope_with_LLM.

• The paper shows that disrupting massive values in the Q and K components significantly degrades performance in tasks requiring contextual understanding.
• It demonstrates that Rotary Positional Encoding drives the emergence of concentrated massive values in low-frequency regions of Q and K, enhancing semantic encoding.
• The findings stress the need for quantization techniques that protect massive values, as seen with AWQ and SmoothQuant outperforming methods like GPTQ.

Massive Values in Self-Attention and Contextual Knowledge

This paper investigates the role of concentrated massive values within the self-attention modules of LLMs, focusing on their impact on contextual knowledge understanding. The research demonstrates that these massive values, primarily located in the query (Q) and key (K) components of the attention mechanism, are critical for processing contextual information, while having a limited impact on parametric knowledge retrieval. The paper also identifies Rotary Positional Encoding (RoPE) as a key factor contributing to the emergence and concentration of these massive values.

Identification and Distribution of Massive Values

The paper begins by defining and identifying massive values within the attention queries (Q) and keys (K) in LLMs. Using the $L_2$ norm along the sequence length dimension, a matrix $M \in \mathbb{R}^{\mathcal{H} \times \mathcal{D}}$ is computed, where $\mathcal{H}$ is the number of attention heads and $\mathcal{D}$ is the head dimension. A massive value is then defined as an element $M_{h, d}$ that significantly exceeds the average value across all dimensions in a given head.

The research highlights that massive values are not uniformly distributed. Instead, they concentrate in specific regions of Q and K (Figure 1), a phenomenon not observed in the value (V) component. This concentration is further characterized by clustering at similar positional indices across different attention heads, suggesting a coordinated role in the attention mechanism.

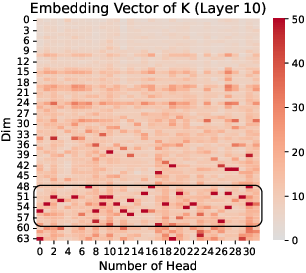
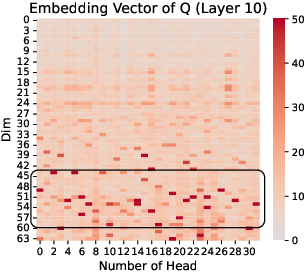
Figure 1: Q and K Embedding Vector in Llama-2-7B, we choose Layer 10 and 20, and the input question is shown as \autoref{fig:prompt_in_inference_LLM}.

Impact on Contextual vs. Parametric Knowledge

The paper differentiates between two types of knowledge utilized by LLMs: contextual knowledge (CK), derived from the current context window, and parametric knowledge (PK), encoded within the model's parameters during pre-training. To assess the role of massive values in these knowledge domains, the researchers conducted experiments disrupting massive values and non-massive values in Q and K during the prefilling stage of LLM inference. Disrupting the decode stage compromises the model's fundamental LLMing capabilities.

The results demonstrate a clear distinction: disrupting massive values leads to a significant degradation in tasks requiring contextual knowledge understanding, such as passkey retrieval, IMDB review analysis, and mathematical reasoning. In contrast, tasks relying on parametric knowledge, such as factual question answering about world cities, are only subtly affected. Specifically, GSM8K accuracy drops dramatically, and Passkey Retrieval tasks collapse from 100\% to near-zero accuracy. Perplexity analysis further supports these findings, showing a marked increase in perplexity for contextual understanding tasks when massive values are disrupted (Figure 2).

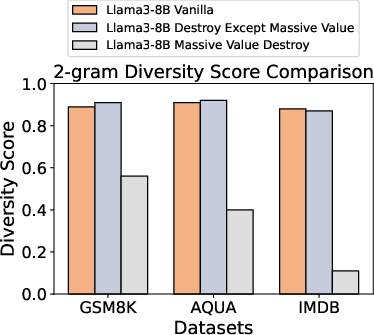
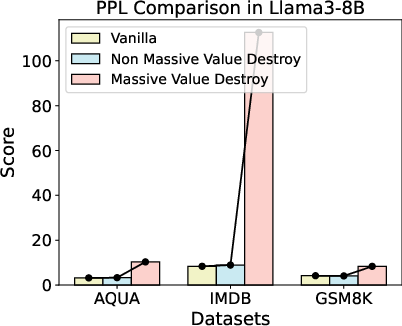
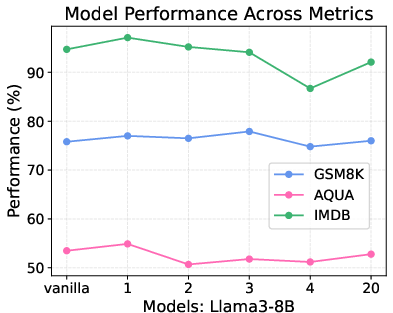
Figure 2: When massive values are disrupted, it significantly reduces diversity and increases perplexity, especially in the IMDB dataset, suggesting poorer performance. Conversely, the vanilla model and the model when non-massive values are disrupted can still achieve lower perplexity and higher diversity.

Further experiments involving the introduction of conflicting contextual information in factual datasets reveal that disrupting massive values can cause the model to default to its parametric knowledge, effectively ignoring the contradictory context (Figure 3). This suggests that massive values are critical for integrating and processing contextual cues, while parametric knowledge retrieval relies on distinct mechanisms.

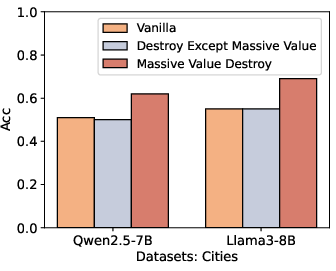
Figure 3: We can observe that introducing conflicting background knowledge causes LLM to be misled into making random guesses. However, after massive values are disrupted, the model is still able to maintain a certain level of accuracy.

Implications for Quantization Techniques

The paper explores the implications of these findings for model quantization, a technique used to reduce the memory footprint and computational cost of LLMs. The experiments evaluate three quantization methods: AWQ, SmoothQuant, and GPTQ. AWQ and SmoothQuant, which explicitly preserve massive values during quantization, maintain strong performance across all tasks. AWQ achieves this by selectively protecting "important" weights during quantization. SmoothQuant employs a smoothing factor ($S$) to redistribute massive values in activations. GPTQ, which does not specifically protect massive values, exhibits significant performance degradation on contextual knowledge understanding tasks, particularly on GSM8K and AQUA (Figure 4). This highlights that quantization strategies must account for massive values to preserve contextual understanding capabilities.

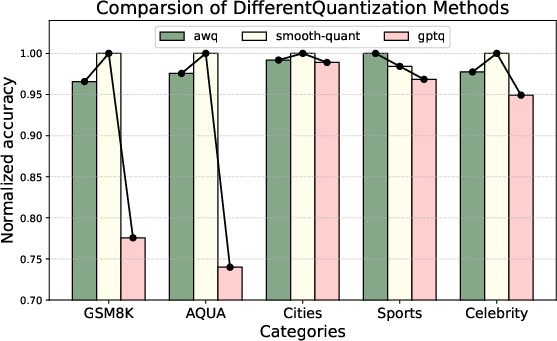
Figure 4: Impacts of different quantization methods on Llama3-8b across different benchmarks.

Role of Rotary Positional Encoding (RoPE)

The research identifies RoPE as a key factor in the emergence and concentration of massive values. Through comparative analysis, it is shown that models employing RoPE consistently exhibit concentrated massive values in Q and K, a pattern absent in models without RoPE, such as OPT (Figure 5). Furthermore, the paper notes that RoPE applies position encoding selectively to $K$ and $Q$, but not on $V$ (Figure 6).

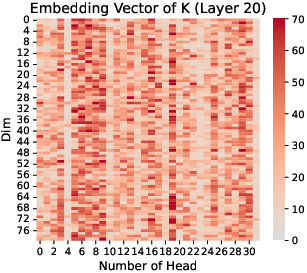
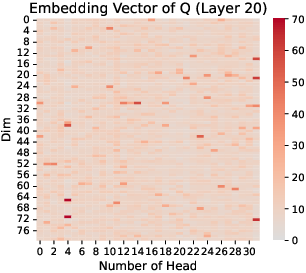
Figure 5: K, Q, V in Layer 20 of OPT-350M.

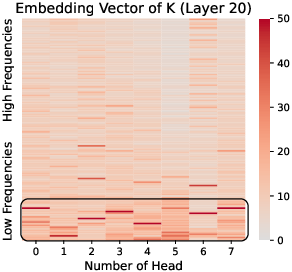
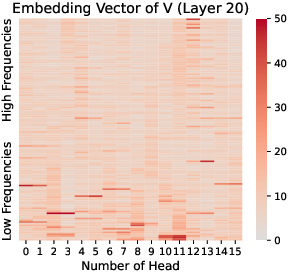
Figure 6: K, Q, and V at Layer 20 in Gemma2-9B. Massive values are notable in low-frequency regions of K and Q, absent in V.

The mechanism of RoPE, which involves rotating dimensions based on their frequency, leads to the concentration of massive values in low-frequency regions of Q and K. This is because low-frequency regions are less affected by position information and encode richer semantic content. The analysis also reveals that the concentrated massive values appear in LLMs with RoPE starting from the very first layer, suggesting that this phenomenon is intrinsic to RoPE's design.

Conclusion

This paper provides empirical evidence for the crucial role of massive values in contextual knowledge understanding within LLMs. The concentration of massive values in Q and K, driven by RoPE, highlights a distinct structural property of these components and emphasizes the importance of accounting for these values in model optimization techniques like quantization. These findings offer insights for designing more efficient and interpretable LLM architectures. Future research directions include exploring alternative positional encoding methods that mitigate the risk of information loss during quantization and investigating the relationship between massive values and specific linguistic phenomena.