Impact of dendritic non-linearities on the computational capabilities of neurons (2407.07572v2)

Abstract: How neurons integrate the myriad synaptic inputs scattered across their dendrites is a fundamental question in neuroscience. Multiple neurophysiological experiments have shown that dendritic non-linearities can have a strong influence on synaptic input integration. These non-linearities have motivated mathematical descriptions of single neuron as a two-layer computational units, which have been shown to increase substantially the computational abilities of neurons, compared to linear dendritic integration. However, current analytical studies are restricted to neurons with unconstrained synaptic weights and unplausible dendritic non-linearities. Here, we introduce a two-layer model with sign-constrained synaptic weights and a biologically plausible form of dendritic non-linearity, and investigate its properties using both statistical physics methods and numerical simulations. We find that the dendritic non-linearity enhances both the number of possible learned input-output associations and the learning velocity. We characterize how capacity and learning speed depend on the implemented non-linearity and the levels of dendritic and somatic inhibition. We calculate analytically the distribution of synaptic weights in networks close to maximal capacity, and find that a large fraction of zero-weight ('silent' or 'potential') synapses naturally emerge in neurons with sign-constrained synapses, as a consequence of non-linear dendritic integration. Non-linearly induced sparsity comes with a second central advantage for neuronal information processing, i.e. input and synaptic noise robustness. We test our model on standard real-world benchmark datasets and observe empirically that the non-linearity provides an enhancement in generalization performance, showing that it enables to capture more complex input/output relations.

• The paper demonstrates that dendritic non-linearities significantly boost storage capacity compared to linear models, with saturating functions yielding linear divergence at high thresholds.
• The paper employs analytical replica methods alongside SGD and LAL evaluations to reveal faster learning speeds and improved robustness against input and synaptic noise.
• The paper shows that biologically realistic dendritic integration naturally induces high synaptic sparsity, aligning with experimental observations in cortical pyramidal cells.

Impact of Dendritic Non-Linearities on the Computational Capabilities of Neurons

Introduction

This work rigorously analyzes the computational consequences of dendritic non-linearities in single-neuron models, focusing on the integration of biologically realistic, sign-constrained synaptic weights and experimentally motivated dendritic transfer functions. The paper leverages both analytical methods from statistical physics and extensive numerical experiments to quantify how dendritic non-linearities—specifically those observed in cortical pyramidal neurons—affect storage capacity, learning dynamics, synaptic sparsity, robustness, and generalization. The model is formalized as a two-layer tree committee machine with non-overlapping dendritic branches, each implementing a non-linear transfer function, and is compared against the classical linear perceptron.

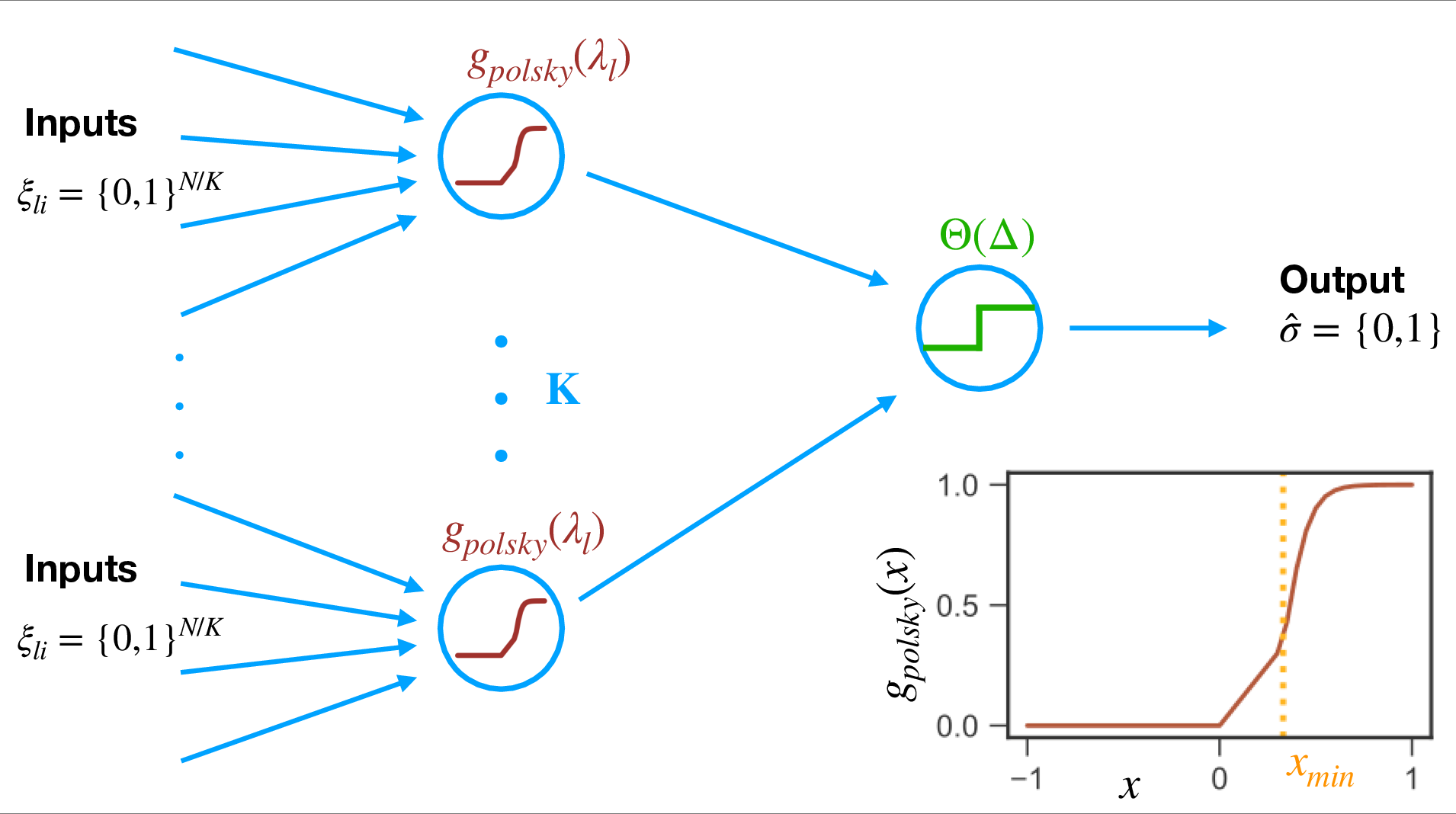
Figure 1: Single-neuron model with dendritic non-linearities. The neuron has $K$ dendritic branches, each summing synaptic inputs linearly and applying a non-linear transfer function before somatic integration.

Model Architecture and Biophysical Constraints

The neuron is modeled as a two-layer network: $N$ binary inputs are distributed across $K$ dendritic branches, each with non-negative (excitatory) synaptic weights. The output of each branch is computed as a non-linear function $g(\cdot)$ of its total input, parameterized to match experimental data (e.g., the Polsky function). The outputs of all branches are summed and compared to a somatic threshold to determine the binary output. Inhibitory effects are incorporated into dendritic and somatic thresholds, and only excitatory synapses are plastic.

The dendritic non-linearity is critical: the Polsky function captures the experimentally observed regime of linear summation at low input, strong non-linearity above a threshold, and saturation at high input. This function interpolates between ReLU and step-like non-linearities, allowing systematic exploration of the impact of non-linearity shape on computational properties.

Storage Capacity: Analytical and Algorithmic Perspectives

Statistical Physics Analysis

The storage capacity, defined as the maximal number of random input-output associations that can be learned (critical capacity $\alpha_c$), is computed using the replica method in the replica symmetric (RS) approximation. The analysis is performed in the biologically relevant regime of large $N$ and $K$ with $K/N \to 0$. The critical capacity is shown to depend sensitively on the dendritic and somatic thresholds, as well as the specific form of the dendritic non-linearity.

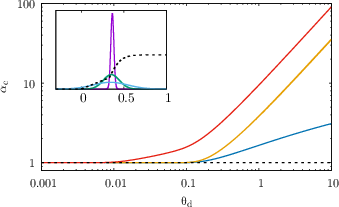
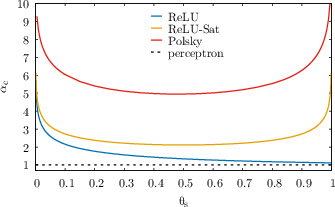
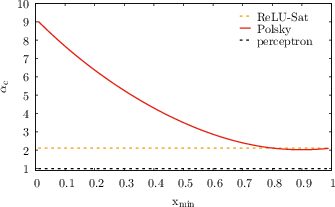
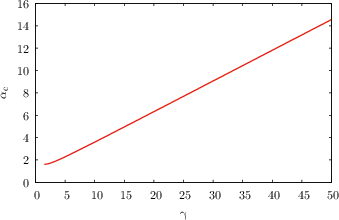
Figure 2: Critical capacities $\alpha_c$ for ReLU, saturating ReLU, and Polsky non-linearities as a function of dendritic and somatic thresholds. The dashed line is the one-layer perceptron baseline.

Key findings include:

• For linear dendritic integration, $\alpha_c$ is independent of the dendritic threshold and matches the classical perceptron result ($\alpha_c^{\text{perc}} = 1$ for $f_{\text{in}} = f_{\text{out}} = 0.5$).
• For non-linear dendritic integration, $\alpha_c$ increases with the dendritic threshold, with saturating non-linearities (e.g., Polsky) yielding a much steeper increase than non-saturating ones (e.g., ReLU).
• In the limit of large dendritic threshold, the capacity diverges linearly for saturating non-linearities and only logarithmically for ReLU.

Algorithmic Capacity and Learning Speed

The practical capacity achievable by learning algorithms (SGD and LAL) is evaluated. For the non-linear neuron, both SGD and LAL surpass the perceptron’s capacity, with LAL achieving higher capacities at large dendritic thresholds. However, the algorithmic capacity remains below the RS analytical bound, especially at high thresholds, indicating algorithmic hardness and possible replica symmetry breaking (RSB) effects.

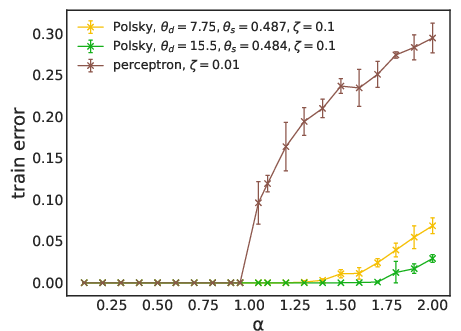
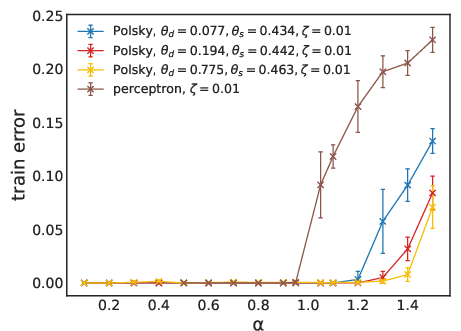
Figure 3: Fraction of misclassified patterns as a function of pattern load $\alpha$ for linear and non-linear neurons, using LAL (top) and SGD (bottom). Non-linear models exceed the perceptron’s maximal capacity.

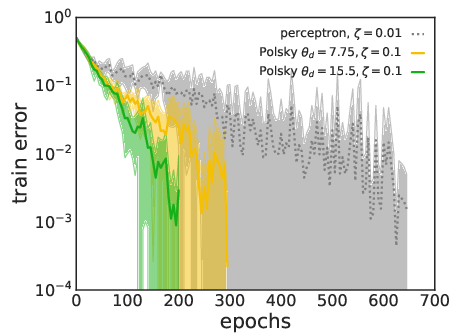
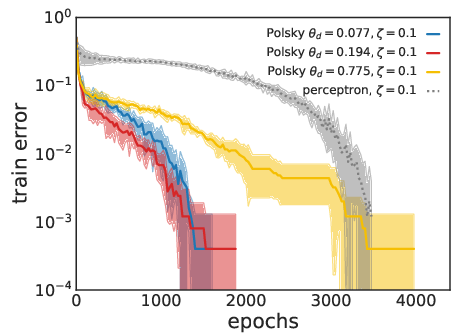
Figure 4: Training speed comparison. Non-linear neurons converge faster than linear ones for both LAL (top) and SGD (bottom) at matched parameter counts.

Figure 5: Algorithmic capacity for LAL and SGD as a function of dendritic threshold, compared to the analytical RS estimate. The perceptron’s critical capacity is shown as a dashed line.

Synaptic Weight Distribution and Sparsity

A central result is that dendritic non-linearities induce high synaptic sparsity (fraction of silent synapses) even in the absence of explicit robustness constraints. The distribution of synaptic weights at maximal capacity is a mixture of a delta function at zero and a truncated Gaussian for positive weights, matching experimental observations in cortical pyramidal cells.

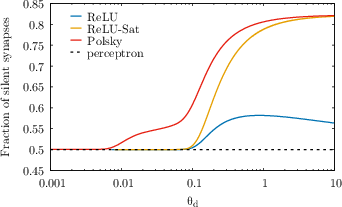
Figure 6: Fraction of silent synapses at maximal capacity as a function of dendritic threshold for Polsky, ReLU, and ReLU-Sat non-linearities. The linear model remains at 0.5.

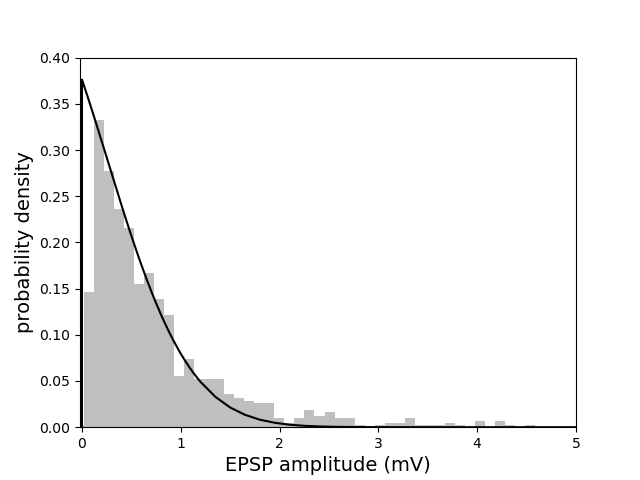
Figure 7: Experimental distribution of synaptic weights (from [song2005highly]) vs. theoretical distribution at maximal capacity, fitted by adjusting dendritic and somatic thresholds.

The model reproduces experimentally observed connection probabilities and weight distributions without requiring a robustness margin, in contrast to linear models. The fraction of silent synapses increases with dendritic threshold for saturating non-linearities, and the Polsky function maintains high sparsity even at large thresholds.

Robustness to Noise and Generalization

The non-linear neuron exhibits enhanced robustness to both input and synaptic noise compared to the linear model. This is quantified by measuring the increase in training error under input bit flips and multiplicative synaptic perturbations.

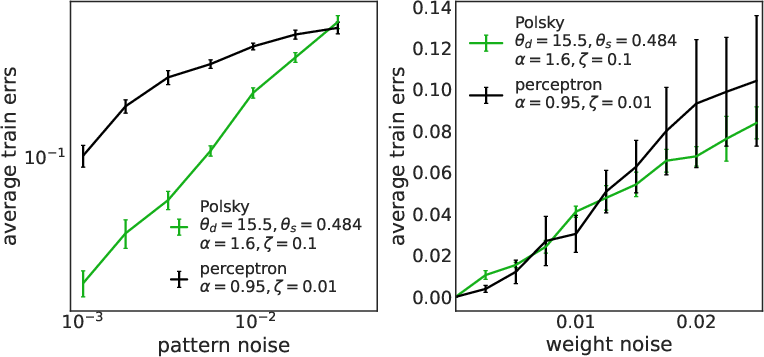
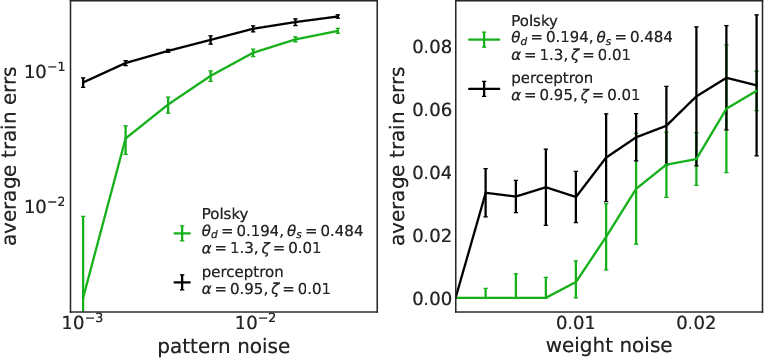
Figure 8: Robustness to input (left) and synaptic (right) noise for LAL (top) and SGD (bottom). Non-linear neurons are consistently more robust.

Generalization performance is evaluated on binarized versions of MNIST, Fashion-MNIST, and CIFAR-10. The non-linear neuron achieves lower test errors than the linear model across all datasets and learning algorithms, demonstrating its ability to capture more complex input-output relations.

(Figure 9)

Figure 9: Generalization error on MNIST, Fashion-MNIST, and CIFAR-10 for SGD (left) and LAL (right). Non-linear neurons outperform linear ones in all cases.

Theoretical and Practical Implications

The results establish that dendritic non-linearities confer several computational advantages:

• Increased storage capacity: Non-linear dendritic integration allows a single neuron to store more associations than a linear perceptron, with the gain depending on the non-linearity’s shape and thresholds.
• Induced sparsity: High levels of synaptic sparsity emerge naturally, matching experimental data, without the need for explicit robustness constraints.
• Faster and more robust learning: Non-linear neurons learn faster and are more robust to noise, both at the input and synaptic level.
• Improved generalization: The model generalizes better on real-world tasks, indicating an increased representational power.

These findings have implications for both neuroscience and artificial intelligence. In neuroscience, they provide a quantitative framework for understanding the computational role of dendritic non-linearities and synaptic sparsity. In AI, they suggest that incorporating biologically inspired non-linearities and architectural constraints can enhance the efficiency and robustness of single-unit models.

Limitations and Future Directions

The paper is limited to two-layer architectures with non-overlapping dendritic branches and does not model inhibitory plasticity or input correlations. The analytical results rely on the RS approximation, and the gap between algorithmic and analytical capacity suggests the need for RSB analysis. Future work should explore deeper dendritic hierarchies, more realistic inhibitory mechanisms, and unsupervised learning scenarios. Additionally, the development of biologically plausible plasticity rules for non-linear dendritic architectures remains an open challenge.

Conclusion

This work demonstrates that dendritic non-linearities substantially enhance the computational capabilities of single neurons, increasing storage capacity, inducing biologically realistic sparsity, improving learning speed and robustness, and enabling better generalization. These results bridge the gap between biophysical realism and computational power, providing a rigorous foundation for future studies of single-neuron computation and its implications for both neuroscience and machine learning.