Language models scale reliably with over-training and on downstream tasks (2403.08540v2)

Abstract: Scaling laws are useful guides for derisking expensive training runs, as they predict performance of large models using cheaper, small-scale experiments. However, there remain gaps between current scaling studies and how LLMs are ultimately trained and evaluated. For instance, scaling is usually studied in the compute-optimal training regime (i.e., "Chinchilla optimal" regime). In contrast, models are often over-trained to reduce inference costs. Moreover, scaling laws mostly predict loss on next-token prediction, but models are usually compared on downstream task performance. To address both shortcomings, we create a testbed of 104 models with 0.011B to 6.9B parameters trained with various numbers of tokens on three data distributions. First, we fit scaling laws that extrapolate in both the amount of over-training and the number of model parameters. This enables us to predict the validation loss of a 1.4B parameter, 900B token run (i.e., 32$\times$ over-trained) and a 6.9B parameter, 138B token run (i.e., a compute-optimal run)$\unicode{x2014}$each from experiments that take 300$\times$ less compute. Second, we relate the perplexity of a LLM to its downstream task performance by proposing a power law. We use this law to predict top-1 error averaged over downstream tasks for the two aforementioned models, using experiments that take 20$\times$ less compute. Our experiments are available at https://github.com/mlfoundations/scaling.

Scaling Laws for Over-trained LLMs and Downstream Task Prediction

Introduction to Scaling in Over-trained Regime and Downstream Performance Prediction

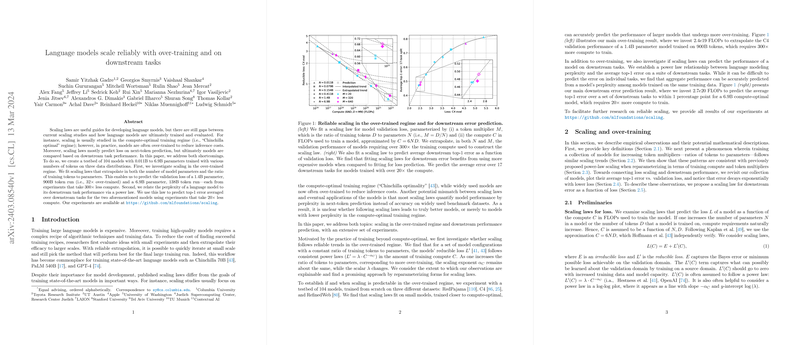
In the field of machine learning, particularly within the paper of LLMs (LMs), understanding the behavior of models as they scale is crucial for both theoretical insight and practical application. Recent research has taken significant strides toward mapping the landscape of how LLMs scale, especially under the lens of compute and parameter size optimization, known as the "Chinchilla optimal" regime. However, a gap persists in our understanding, particularly regarding models that are over-trained to reduce inference costs and how these scaling laws translate into performance on downstream tasks rather than merely predicting next-token perplexity.

This analysis aims to bridge these gaps by conducting an extensive set of experiments characterizing the behavior of LLMs when over-trained and evaluating their performance on downstream tasks. Through the examination of 104 models, ranging from 0.011B to 6.9B parameters, trained with varying numbers of tokens and on different data distributions, we derive and validate scaling laws that accurately predict both over-trained model performance and downstream task effectiveness.

Over-training and Its Predictable Nature

Investigating the over-trained regime, we discovered that models display consistent scaling trends even when the training data volume significantly exceeds the compute-optimal level. Our analyses demonstrate that both the validation loss and the downstream task performance of these models can be accurately predicted by fitting scaling laws to small-scale experimental data. Notably, the paper made successful predictions about the performance of exceptionally large-scale models (1.4B and 6.9B parameters), significantly reducing the computational expense required for direct evaluation.

Implications for Downstream Task Performance

Furthermore, we present a novel relationship between the perplexity of a LLM and its performance on downstream tasks, framed within a power-law context. This finding is pivotal as it allows for the prediction of downstream performance solely from a model's perplexity, thereby offering a computationally efficient approach to estimate the practical utility of LLMs in real-world applications.

Theoretical and Practical Contributions

Theoretically, this work enhances our understanding of LLM behavior in the over-trained regime, offering insights into how and why these models scale as they do. Practically, it provides a valuable tool for predicting downstream task performance, significantly impacting the development and application of LLMs by enabling more efficient resource allocation during training.

Future Directions

This research opens several avenues for future exploration, including refining the scaling laws to incorporate the effects of hyperparameter choices, validating the current findings with even larger models, and extending these laws to predict model performance on individual downstream tasks. Moreover, investigating the application of these scaling laws in the context of models fine-tuned with supervised or reinforcement learning methods could further augment their utility in applied settings.

Conclusion

Our experiments contribute landmark findings to the field of LLM scaling by meticulously detailing the scaling behavior of over-trained models and relating model perplexity to downstream task performance in a quantifiable manner. These contributions not only advance our theoretical understanding of LLM scaling laws but also offer practical tools for predicting the performance of these models in real-world applications.