VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation

Abstract: Behavior prediction in dynamic, multi-agent systems is an important problem in the context of self-driving cars, due to the complex representations and interactions of road components, including moving agents (e.g. pedestrians and vehicles) and road context information (e.g. lanes, traffic lights). This paper introduces VectorNet, a hierarchical graph neural network that first exploits the spatial locality of individual road components represented by vectors and then models the high-order interactions among all components. In contrast to most recent approaches, which render trajectories of moving agents and road context information as bird-eye images and encode them with convolutional neural networks (ConvNets), our approach operates on a vector representation. By operating on the vectorized high definition (HD) maps and agent trajectories, we avoid lossy rendering and computationally intensive ConvNet encoding steps. To further boost VectorNet's capability in learning context features, we propose a novel auxiliary task to recover the randomly masked out map entities and agent trajectories based on their context. We evaluate VectorNet on our in-house behavior prediction benchmark and the recently released Argoverse forecasting dataset. Our method achieves on par or better performance than the competitive rendering approach on both benchmarks while saving over 70% of the model parameters with an order of magnitude reduction in FLOPs. It also outperforms the state of the art on the Argoverse dataset.

• The paper presents VectorNet, a model that encodes HD maps and agent trajectories using hierarchical graph neural networks to enhance prediction accuracy.
• It leverages polyline subgraphs for local feature extraction and self-attention for global context, significantly reducing computational costs and model parameters.
• Experimental results on the Argoverse dataset show that VectorNet achieves lower Average Displacement Error and outperforms traditional ConvNet approaches.

VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation

Introduction

The paper "VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation" (2005.04259) focuses on behavior prediction in dynamic, multi-agent systems, particularly self-driving vehicles. It introduces the VectorNet model, which leverages a hierarchical graph neural network to predict vehicle trajectories by integrating agent dynamics with HD map context. Unlike previous methods that use rasterized images and ConvNets, VectorNet operates directly on vectorized representations of map and trajectory data, enhancing computational efficiency without sacrificing prediction performance.

Figure 1: Illustration of the rasterized rendering (left) and vectorized approach (right) to represent high-definition map and agent trajectories.

Methodology

VectorNet utilizes a hierarchical graph neural network for encoding structured HD maps and agent trajectories. The vectorized representation captures spatial and semantic locality, treating vectors as graph nodes with features comprising start and end coordinates, semantic labels, and polyline group identifiers. A polyline subgraph aggregates features locally before passing them to a global interaction graph.

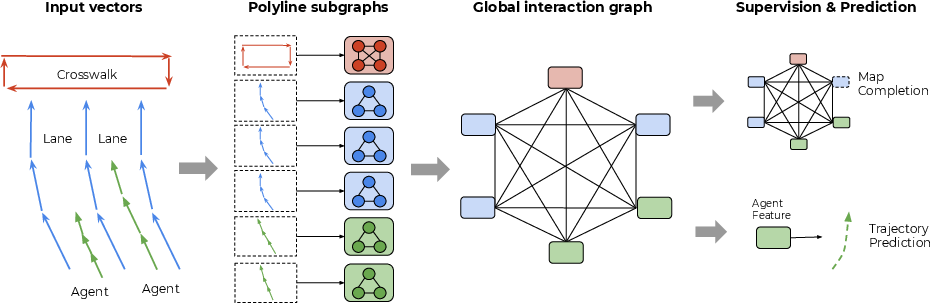
Figure 2: An overview of our proposed VectorNet. Observed agent trajectories and map features are represented as sequences of vectors, which are passed to a local graph network for polyline-level feature extraction.

Key to VectorNet’s success is its hierarchical architecture, where local context is modeled within subgraphs, and global context is captured through self-attention networks. Additionally, a self-supervised auxiliary task of node feature completion enhances the model's ability to infer interactions among entities by reconstructing masked node features based on surrounding context.

Experimental Results

Evaluations were conducted on an in-house behavior prediction benchmark and the Argoverse dataset, demonstrating VectorNet’s competitive performance. VectorNet achieved comparable or superior results compared to baseline ConvNet approaches, reducing computational costs by an order of magnitude and saving over 70% in model parameters while outperforming state-of-the-art methods on Argoverse.

The paper reported significant improvements in Average Displacement Error (ADE) and Displacement Error at varying prediction horizons (DE@n), indicating the model's proficiency in long-term trajectory forecasting. These results underscore VectorNet's robust prediction capabilities and computational efficiency.

Implications and Future Work

VectorNet's approach to encoding vectorized map and trajectory data establishes a promising direction for behavior prediction models, particularly in autonomous driving contexts. Its reduced computational footprint and superior performance make it a feasible option for real-time applications.

The paper hints at potential integrations with multimodal trajectory decoders to extend VectorNet's capabilities in generating diverse future trajectories. Future research might explore these integrations as well as enhancements in vector representation to accommodate even more complex road entity interactions.

Conclusion

The VectorNet model represents a substantial advance in behavior prediction systems, capable of encoding complex map and agent dynamics efficiently through vectorized representations and hierarchical graph architectures. Its application to self-driving vehicles not only advances state-of-the-art trajectory prediction but also paves the way for further innovation in multi-agent system behaviors.

Figure 3: The computation flow on the vector nodes of the same polyline.