MathOPEval: A Fine-grained Evaluation Benchmark for Visual Operations of MLLMs in Mathematical Reasoning (2507.18140v1)
Abstract: Recent progress in Multi-modal LLMs (MLLMs) has enabled step-by-step multi-modal mathematical reasoning by performing visual operations based on the textual instructions. A promising approach uses code as an intermediate representation to precisely express and manipulate the images in the reasoning steps. However, existing evaluations focus mainly on text-only reasoning outputs, leaving the MLLM's ability to perform accurate visual operations via code largely unexplored. This work takes a first step toward addressing that gap by evaluating MLLM's code-based capabilities in multi-modal mathematical reasoning.Specifically, our framework focuses on two key evaluation aspects: (1) Multi-modal Code Generation (MCG) evaluates the model's ability to accurately understand and construct visualizations from scratch. (2) Multi-modal Code Editing (MCE) assesses the model's capacity for fine-grained operations, which include three types: Deletion, Modification and Annotation. To evaluate the above tasks, we incorporate a dataset that covers the five most popular types of mathematical figures, including geometric diagrams, function plots, and three types of statistical charts, to provide a comprehensive and effective measurement of existing MLLMs. Our experimental evaluation involves nine mainstream MLLMs, and the results reveal that existing models still lag significantly behind human performance in performing fine-grained visual operations.
Summary
- The paper introduces MathOPEval as a novel benchmark to assess MLLMs' capability in generating and editing Python/LaTeX code for precise visual operations in mathematical reasoning.
- It constructs a curated dataset of 17,845 items across five mathematical visualization types using both multiple-choice and free-form evaluation formats.
- Experimental results expose substantial performance gaps in code manipulation and spatial reasoning, underscoring challenges despite advanced prompting strategies.
MathOPEval: Fine-grained Evaluation of Visual Operations in MLLMs for Mathematical Reasoning
Motivation and Problem Formulation
The paper introduces MathOPEval, a benchmark designed to rigorously evaluate the visual operation capabilities of Multi-modal LLMs (MLLMs) in mathematical reasoning. While recent advances in MLLMs have enabled stepwise multi-modal reasoning, most existing benchmarks focus on text-only outputs, neglecting the critical intermediate step of code-based visual operations. The authors argue that code—specifically Python (Matplotlib) or LaTeX—serves as a precise, interpretable intermediate representation for visual reasoning, enabling fine-grained assessment of a model's ability to manipulate and generate mathematical visualizations.
MathOPEval targets two primary tasks:
- Multi-modal Code Generation (MCG): Given an image, generate code that reconstructs the image.
- Multi-modal Code Editing (MCE): Given an initial image, its code, and a target (edited) image, generate code that transforms the initial image into the target via deletion, modification, or annotation.
This formulation enables the evaluation of both the model's visual understanding and its ability to perform structured, interpretable visual operations.
Dataset Construction and Task Coverage
The benchmark is built on a manually curated dataset covering five major mathematical visualization types: geometric figures, function plots, bar charts, line graphs, and pie charts. For each visualization, four states are constructed: original, deleted, modified, and annotated, each with corresponding code and instructions.
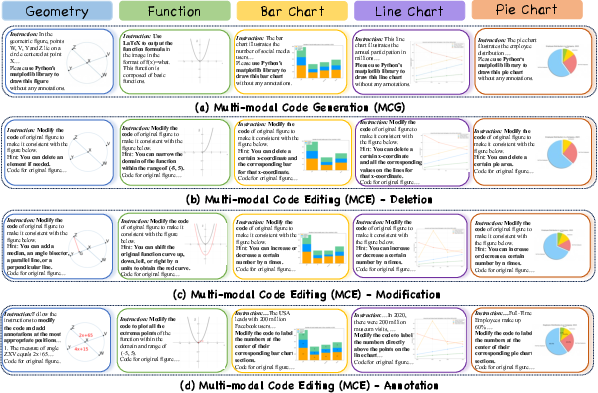
Figure 1: The initial dataset includes instructions, code, and images for four visual operations across five visualization types.
The dataset is further transformed into two evaluation formats: multiple-choice (with distractors) and free-form generation. The total dataset comprises 17,845 questions, with 7,552 open-ended and 10,293 multiple-choice items, ensuring broad coverage of both low-level and high-level visual reasoning skills.
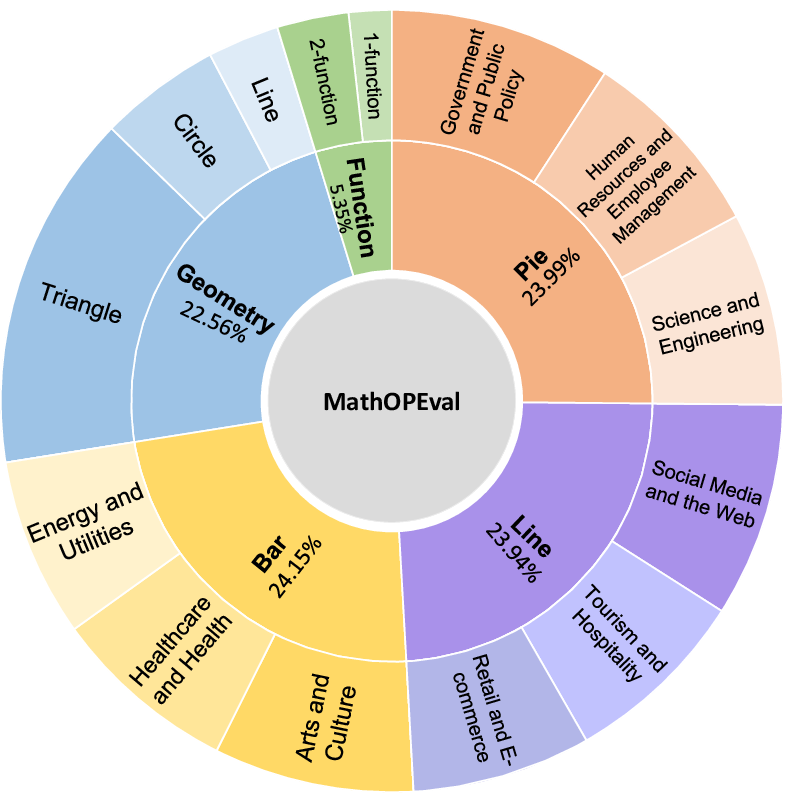
Figure 2: Distribution of visualization types and their context domains, demonstrating the dataset's diversity.
Automated Chain-of-Thought Evaluation
A key contribution is the development of an automated Chain-of-Thought (CoT) evaluation strategy for free-form code generation tasks. The evaluation pipeline consists of:
- Key Element Extraction: The evaluator model (DeepSeek-V3) extracts task-relevant elements (e.g., bar heights, geometric components, function expressions) from both generated and reference code.
- Analytical Scoring: Outputs are scored on a 1–10 scale across content accuracy, positional consistency, code correctness, and completeness, with detailed criteria per visualization and task type.
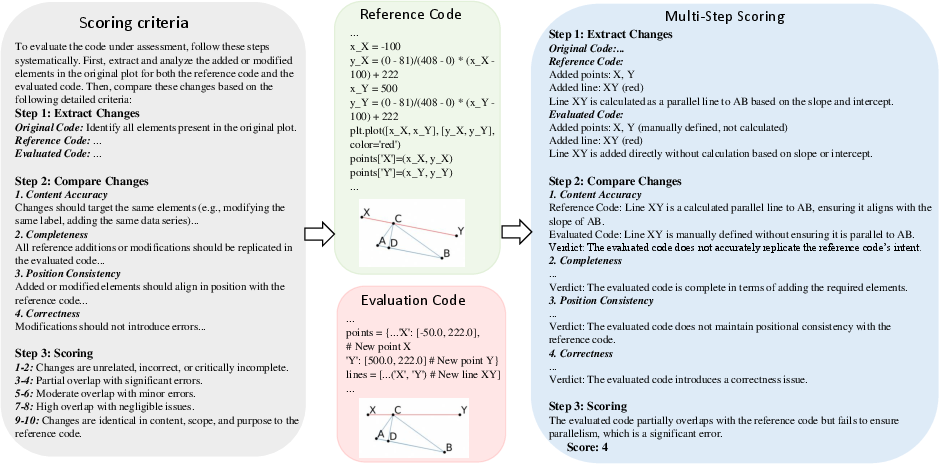
Figure 3: Example of CoT-based evaluation for MCE (Modification) in geometric figures, illustrating key element extraction and multi-dimensional scoring.
Human validation indicates a 92% agreement rate with the automated scores, supporting the reliability of the evaluation protocol.
Experimental Results and Analysis
The benchmark is used to evaluate nine mainstream MLLMs, including GPT-4o, Qwen-VL-Max, Qwen2.5-VL, Gemma3, LLaVA-NeXT, and specialized reasoning models. Several prompting strategies are compared: Direct, CoT, Descriptive CoT (DCoT), and Visualization-of-Thought (VoT).
Key Findings
- Substantial Model-Human Gap: All models exhibit a large performance gap relative to human baselines, with an average gap of 52.39% and up to 67.13% for geometric deletion tasks.
- Task Difficulty: Code modification is the most challenging operation (average accuracy 42.15% in multiple-choice, 2.54/10 in free-form), while annotation is the easiest.
- Visualization Type Sensitivity: Function plots are the most difficult visualization type for all models, with geometric figures also posing significant challenges.
- Prompting Strategy: Contrary to prior work, Direct prompting outperforms CoT and DCoT, likely due to the spatial complexity of mathematical visualizations.
- Scaling Effects: Larger models generally perform better, but scaling does not guarantee improvement on all sub-tasks (e.g., y-intercept identification).
- In-Context Learning: Increasing the number of shots improves performance up to a point (typically 2 shots), after which performance degrades due to context window limitations and increased task ambiguity.
Fine-grained Error and Capability Analysis
The authors provide a detailed breakdown of model errors and capabilities:
- Error Taxonomy: Visual perception errors dominate (86%), followed by instruction comprehension and output format violations (6% each), and reasoning process errors (2%).
- Annotation Subtasks: Models perform better on angle annotations than line labels in geometric figures, and better on extreme points than intercepts in function plots.
- Forward vs. Backward Reasoning: Backward questions (identifying elements from annotations) are easier for models than forward questions (inferring annotations from elements), likely due to the explicit numerical anchors in the former.
- Reasoning-enhanced vs. General Models: Reasoning-enhanced models (e.g., QVQ-72B) show selective improvements, excelling in function code generation and line chart deletion but not universally outperforming general models.
Prompt Design for Evaluation
The benchmark includes carefully designed prompts for each task and visualization type, supporting both multiple-choice and free-form code generation. Prompts are tailored to elicit specific reasoning behaviors, including stepwise CoT, descriptive reasoning, and visualization-of-thought.

Figure 4: Prompt for scoring multi-modal code generation on bar charts.

Figure 5: Prompt for scoring multi-modal code generation on line charts.

Figure 6: Prompt for scoring multi-modal code generation on pie charts.

Figure 7: Prompt for scoring multi-modal code generation on geometric figures.

Figure 8: Prompt for scoring multi-modal code generation on function plots.

Figure 9: Prompt for scoring multi-modal code annotation.

Figure 10: Prompt for scoring multi-modal code deletion.

Figure 11: Prompt for scoring multi-modal code modification.
Implications and Future Directions
MathOPEval exposes the current limitations of MLLMs in performing interpretable, code-based visual operations for mathematical reasoning. The results indicate that:
- Current MLLMs are not yet reliable for fine-grained visual reasoning tasks requiring precise code manipulation.
- Scaling and reasoning-specific training yield only partial improvements, with persistent weaknesses in visual perception and spatial reasoning.
- Prompt engineering and in-context learning can provide moderate gains, but are insufficient to close the gap with human performance.
The benchmark provides a foundation for future research in several directions:
- Model Alignment: Leveraging MathOPEval for supervised fine-tuning or reinforcement learning to align MLLMs with code-based visual reasoning objectives.
- Architectural Innovations: Developing architectures with improved visual perception modules and explicit spatial reasoning capabilities.
- Evaluation Expansion: Extending the benchmark to cover additional reasoning skills such as planning, error correction, and reflection in mathematical problem solving.
Conclusion
MathOPEval establishes a rigorous, interpretable, and fine-grained evaluation framework for assessing the visual operation capabilities of MLLMs in mathematical reasoning. The benchmark reveals significant gaps between current models and human-level performance, particularly in tasks requiring precise code-based visual manipulation. The findings underscore the need for targeted model improvements in visual perception, spatial reasoning, and code generation, and provide a valuable resource for the development and evaluation of next-generation multi-modal reasoning systems.
Follow-up Questions
- How does MathOPEval differ from traditional text-based evaluation methods in assessing MLLMs?
- What benefits does using code as an intermediate representation provide in mathematical visual reasoning?
- How might the detailed error taxonomy in MathOPEval guide future improvements in MLLM architectures?
- What impact does prompt engineering and in-context learning have on enhancing MLLM performance in visual operations?
- Find recent papers about MLLM visual reasoning.
Related Papers
- MathVista: Evaluating Mathematical Reasoning of Foundation Models in Visual Contexts (2023)
- MathVerse: Does Your Multi-modal LLM Truly See the Diagrams in Visual Math Problems? (2024)
- Plot2Code: A Comprehensive Benchmark for Evaluating Multi-modal Large Language Models in Code Generation from Scientific Plots (2024)
- ChartMimic: Evaluating LMM's Cross-Modal Reasoning Capability via Chart-to-Code Generation (2024)
- MAVIS: Mathematical Visual Instruction Tuning with an Automatic Data Engine (2024)
- Revisiting Multi-Modal LLM Evaluation (2024)
- Polymath: A Challenging Multi-modal Mathematical Reasoning Benchmark (2024)
- MathGLM-Vision: Solving Mathematical Problems with Multi-Modal Large Language Model (2024)
- Open Eyes, Then Reason: Fine-grained Visual Mathematical Understanding in MLLMs (2025)
- MathCoder-VL: Bridging Vision and Code for Enhanced Multimodal Mathematical Reasoning (2025)