Dynamic Chunking for End-to-End Hierarchical Sequence Modeling (2507.07955v2)

Abstract: Major progress on LMs in recent years has largely resulted from moving away from specialized models designed for specific tasks, to general models based on powerful architectures (e.g. the Transformer) that learn everything from raw data. Despite this trend, pre-processing steps such as tokenization remain a barrier to true end-to-end foundation models. We introduce a collection of new techniques that enable a dynamic chunking mechanism which automatically learns content- and context- dependent segmentation strategies learned jointly with the rest of the model. Incorporating this into an explicit hierarchical network (H-Net) allows replacing the (implicitly hierarchical) tokenization-LM-detokenization pipeline with a single model learned fully end-to-end. When compute- and data- matched, an H-Net with one stage of hierarchy operating at the byte level outperforms a strong Transformer LLM operating over BPE tokens. Iterating the hierarchy to multiple stages further increases its performance by modeling multiple levels of abstraction, demonstrating significantly better scaling with data and matching the token-based Transformer of twice its size. H-Nets pretrained on English show significantly increased character-level robustness, and qualitatively learn meaningful data-dependent chunking strategies without any heuristics or explicit supervision. Finally, the H-Net's improvement over tokenized pipelines is further increased in languages and modalities with weaker tokenization heuristics, such as Chinese and code, or DNA sequences (nearly 4x improvement in data efficiency over baselines), showing the potential of true end-to-end models that learn and scale better from unprocessed data.

• The paper presents H-Net, which introduces a dynamic chunking mechanism for learning content-dependent segmentation without explicit tokenization.
• The architecture follows a U-Net structure with encoder, main, and decoder networks, employing routing and smoothing modules for stable gradient flow.
• Experimental results show that a two-stage H-Net matches or exceeds the performance of BPE-tokenized Transformers on language modeling and downstream tasks.

H-Net: Dynamic Chunking for End-to-End Hierarchical Sequence Modeling

This paper introduces H-Net, a hierarchical neural network architecture that incorporates a dynamic chunking (DC) mechanism to learn content- and context-dependent segmentation strategies for sequence modeling, eliminating the need for explicit tokenization. The authors demonstrate that H-Net outperforms token-based Transformers and other byte-level models across various tasks and modalities.

H-Net Architecture and Dynamic Chunking

The H-Net architecture follows a U-Net structure, consisting of encoder networks ($\mathcal{E}$), a main network ($\mathcal{M}$), and decoder networks ($\mathcal{D}$) (Figure 1). Raw data is processed by the encoder, downsampled via the DC mechanism, processed by the main network, upsampled by a dechunking layer, and then processed by the decoder. The main network can be any standard architecture like a Transformer or SSM. The DC mechanism is composed of a routing module, which predicts boundaries between adjacent elements based on similarity scores, and a smoothing module, which interpolates representations using the router's outputs. The H-Net uses an auxiliary loss function to target desired downsampling ratios, and techniques for gradient-based learning of discrete choices, enabling it to learn how to compress data in a fully end-to-end fashion.

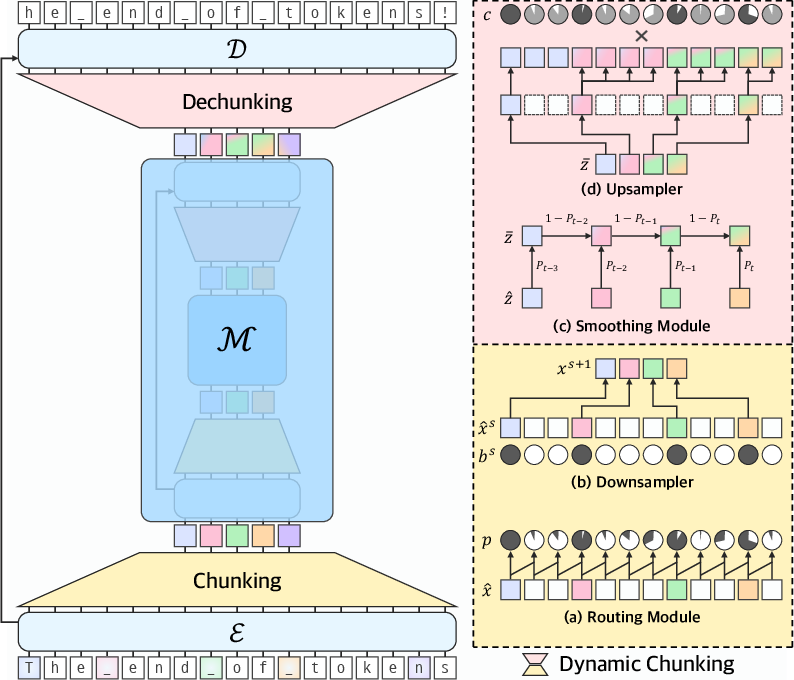
Figure 1: (left) Architectural overview of H-Net with a two-stage hierarchical design (S=2). (right) Dynamic Chunking (DC).

Implementation Details

The routing module calculates boundary probabilities $p_t$ using cosine similarity between adjacent encoder outputs $\hat{x}_t$:

$q_t = W_q \hat{x}_t, \quad k_t = W_k \hat{x}_t, \qquad p_t = \frac{1}{2} \left(1 - \frac{q_t^\top k_{t-1}}{\left\Vert q_t \right\Vert \left\Vert k_{t-1} \right\Vert}\right) \in [0, 1], \quad b_t = \mathds{1}_{\{p_t \geq 0.5\}}$

where $q_t$ and $k_t$ are projections of the encoder outputs. The smoothing module applies an exponential moving average (EMA) to the compressed representations:

$\bar{z}_t = P_t \hat{z}_t + (1-P_t) \bar{z}_{t-1}$

This technique transforms discrete chunking operations into differentiable computations by creating smooth interpolations between chunks. The upsampler decompresses the smoothed representations $\bar{z}^{s+1}$ to match the original resolution of inputs in the previous stage $z^{s}$ using a Straight-Through Estimator (STE) to stabilize gradient flow:

$c_t = p_t^{b_t} (1-p_t)^{1-b_t}$

$$\mathsf{STE}(c_t) = c_t + \text{stopgradient}(1-c_t)$$

$\tilde{z}_t = \bar{z}_{\sum_{k=1}^t b_k}$

$$\mathsf{Upsampler}(\bar{z}, c)_t = \mathsf{STE}\left(c_t\right) \cdot \tilde{z}_t$$

A ratio loss is introduced to guide compression, preventing trivial solutions where the model retains nearly all vectors or compresses excessively:

$$\mathcal{L}_\text{ratio} = \frac{N}{N-1} \left( (N-1) FG + (1-F) (1-G) \right), \qquad F = \frac{1}{L}\sum_{t=1}^{L} b_t, \quad G = \frac{1}{L}\sum_{t=1}^{L} p_t$$

where $F$ is the fraction of vectors selected, $G$ is the average boundary probability, and $N$ controls the target compression ratio.

Experimental Results

The authors conducted experiments on LLMing, evaluating H-Net's performance against tokenized Transformers and other byte-level baselines. Results indicate that a byte-level H-Net matches the perplexity and downstream performance of a strong BPE-tokenized Transformer. Furthermore, the DC module naturally compresses data to a similar resolution as BPE tokenizers (4.5-5 bytes/chunk) and learns meaningful boundaries without external supervision. The authors found that iterating the hierarchy to two stages further improves performance, demonstrating better scaling with data. The two-stage H-Net overtakes the perplexity of a tokenized Transformer after 30B training bytes and matches the downstream evaluations of a tokenized Transformer twice its size.

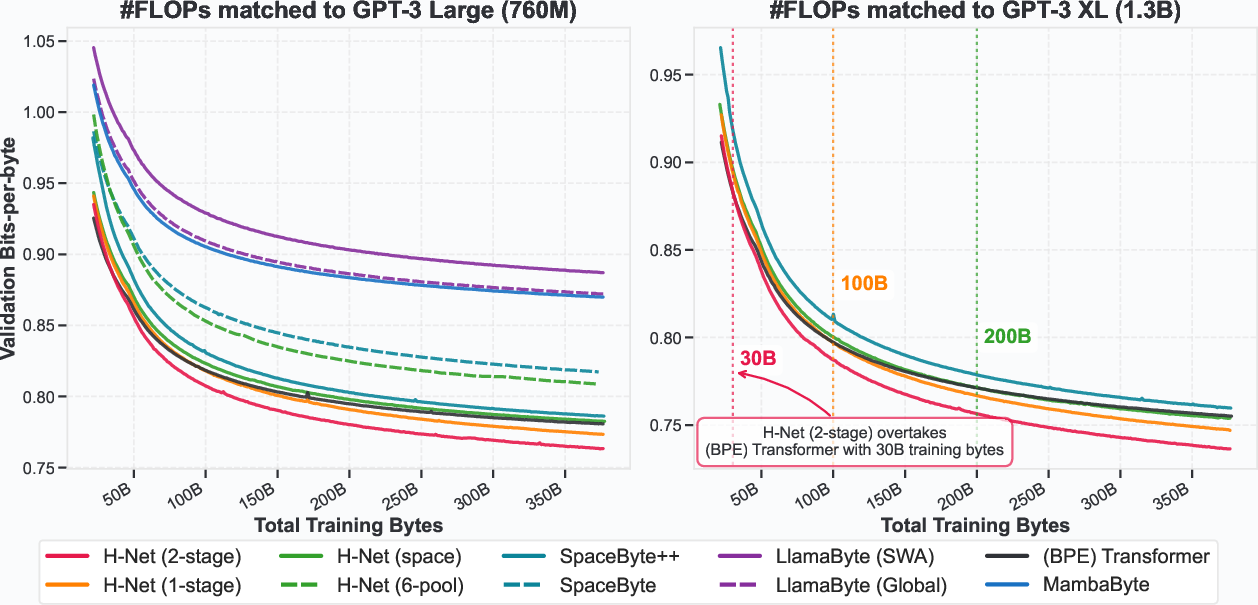
Figure 2: Validation Bits-per-byte (BPB) throughout training for different models at Large (760M, left) and XL (1.3B, right) scales with matched computational and data budgets for training.

Additional experiments demonstrate H-Net's robustness to textual perturbations and its effectiveness on languages without obvious segmentation cues, such as Chinese and code. Ablation studies validate the importance of the smoothing module, similarity-based routing module, and STE for stable training and performance.

Figure 3: Validation Bits-per-byte (BPB) throughout training on Chinese language and code modeling.

Analysis of Learned Boundaries

Visualizations of learned boundaries reveal that H-Net automatically discovers semantically coherent units without explicit supervision. A single-stage H-Net predominantly places boundaries at whitespace characters, similar to SpaceByte, while a two-stage H-Net combines spacelike boundaries with the first few characters of each word. Further analysis shows that H-Net often merges multiple words and spacelike characters based on content, indicating content-aware chunking.

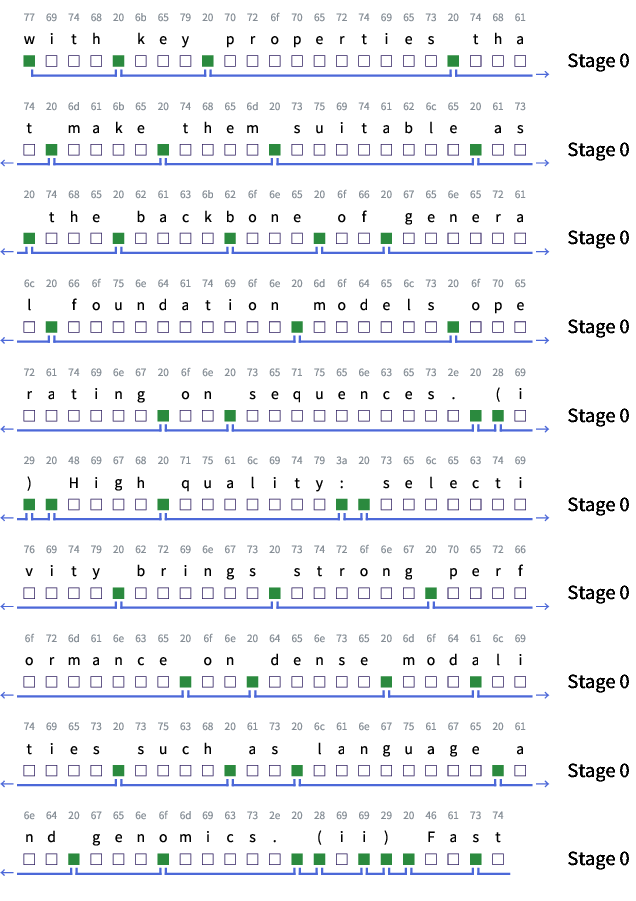
Figure 4: Visualization of boundaries drawn by H-Net.

Implications and Future Directions

The H-Net architecture presents a significant advancement in sequence modeling by eliminating the need for explicit tokenization and learning data-dependent chunking strategies. The ability to learn hierarchical representations from raw data has implications for various NLP tasks and modalities. Future research directions include exploring deeper hierarchies, improving the efficiency of dynamic chunking, and investigating the scaling behavior of H-Net at larger model sizes. The authors suggest that H-Net could serve as a foundation for general foundation models that learn more effectively from unprocessed data.

Conclusion

The paper successfully introduces H-Net, a novel architecture that addresses the limitations of tokenization in sequence modeling. The dynamic chunking mechanism and hierarchical structure enable H-Net to learn meaningful representations from raw data, outperforming traditional token-based models. The results and analysis presented in this paper provide a strong foundation for future research in end-to-end sequence modeling and representation learning.