The Curse of Depth in Large Language Models

Abstract: In this paper, we introduce the Curse of Depth, a concept that highlights, explains, and addresses the recent observation in modern LLMs where nearly half of the layers are less effective than expected. We first confirm the wide existence of this phenomenon across the most popular families of LLMs such as Llama, Mistral, DeepSeek, and Qwen. Our analysis, theoretically and empirically, identifies that the underlying reason for the ineffectiveness of deep layers in LLMs is the widespread usage of Pre-Layer Normalization (Pre-LN). While Pre-LN stabilizes the training of Transformer LLMs, its output variance exponentially grows with the model depth, which undesirably causes the derivative of the deep Transformer blocks to be an identity matrix, and therefore barely contributes to the training. To resolve this training pitfall, we propose LayerNorm Scaling (LNS), which scales the variance of output of the layer normalization inversely by the square root of its depth. This simple modification mitigates the output variance explosion of deeper Transformer layers, improving their contribution. Across a wide range of model sizes (130M to 7B), our experiments show that LNS consistently outperforms previous normalization and scaling techniques in enhancing LLM pre-training performance. Moreover, this improvement seamlessly carries over to supervised fine-tuning. All these gains can be attributed to the fact that LayerNorm Scaling enables deeper layers to contribute more effectively during training. Our code is available at \href{https://github.com/lmsdss/LayerNorm-Scaling}{LayerNorm-Scaling}.

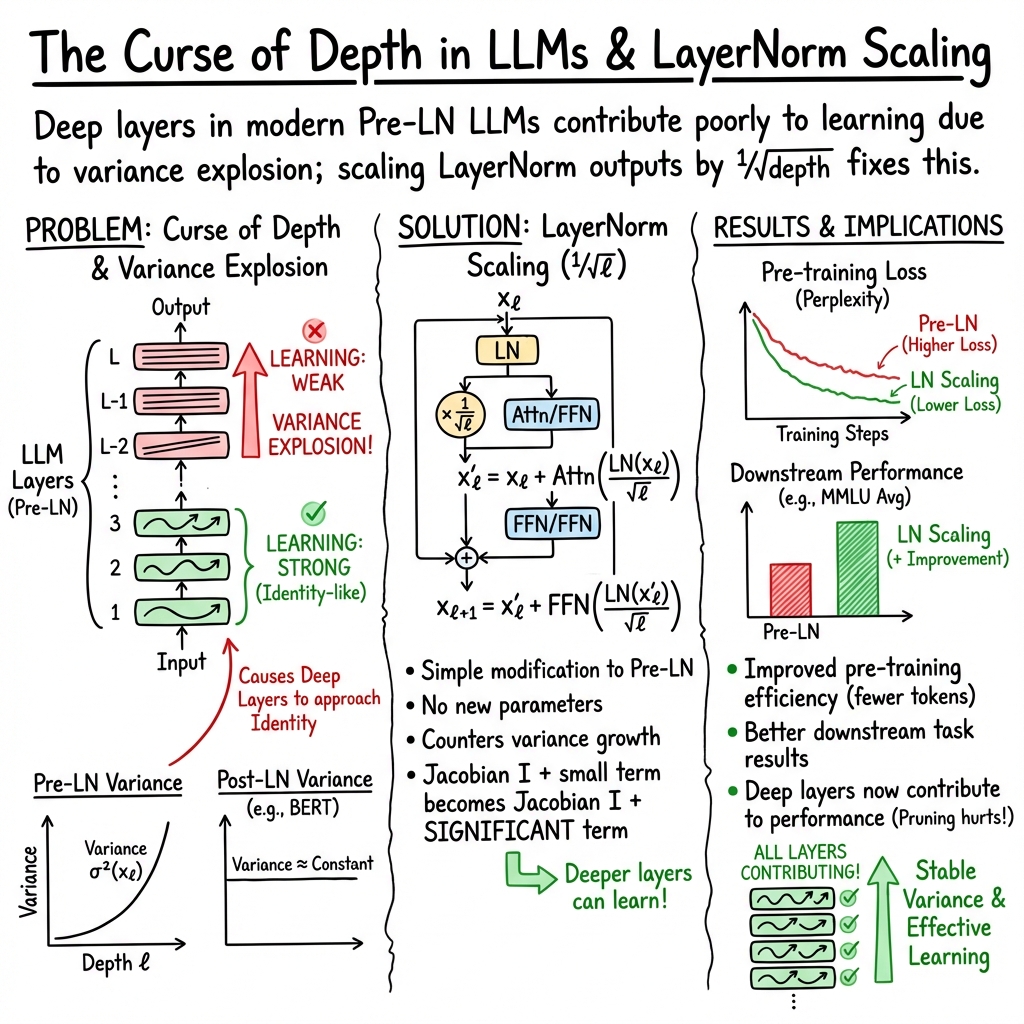
• The paper demonstrates that deeper layers in LLMs using Pre-LN become nearly identity mappings because of exponential output variance growth.
• It provides empirical and theoretical evidence showing that pruning deep transformer layers minimally impacts model performance.
• The introduction of LayerNorm Scaling effectively mitigates variance amplification, enhancing training stability and downstream task accuracy.

The Curse of Depth in LLMs

Introduction

The paper, "The Curse of Depth in LLMs," addresses the phenomenon whereby deeper layers in Transformer-based LLMs often exhibit reduced effectiveness compared to their shallower counterparts. This issue, termed the Curse of Depth (CoD), results from the prevalent use of Pre-Layer Normalization (Pre-LN), which inadvertently causes the variance of output across layers to grow exponentially with depth. This growth stabilizes the training but leads deep transformer blocks to behave almost as identity mappings, thus contributing minimally to learning.

Empirical Evidence and Initial Findings

The research begins with an analysis of several widely-used LLMs, including LLaMA, Mistral, and DeepSeek, to demonstrate the universality of CoD across these models. An empirical approach involving layer pruning was adopted to substantiate this observation. The results reveal that removing deep layers from models like Mistral-7B and Qwen-7B (which use Pre-LN) does not significantly impact performance, while the removal of earlier layers leads to marked performance degradation (Figure 1).

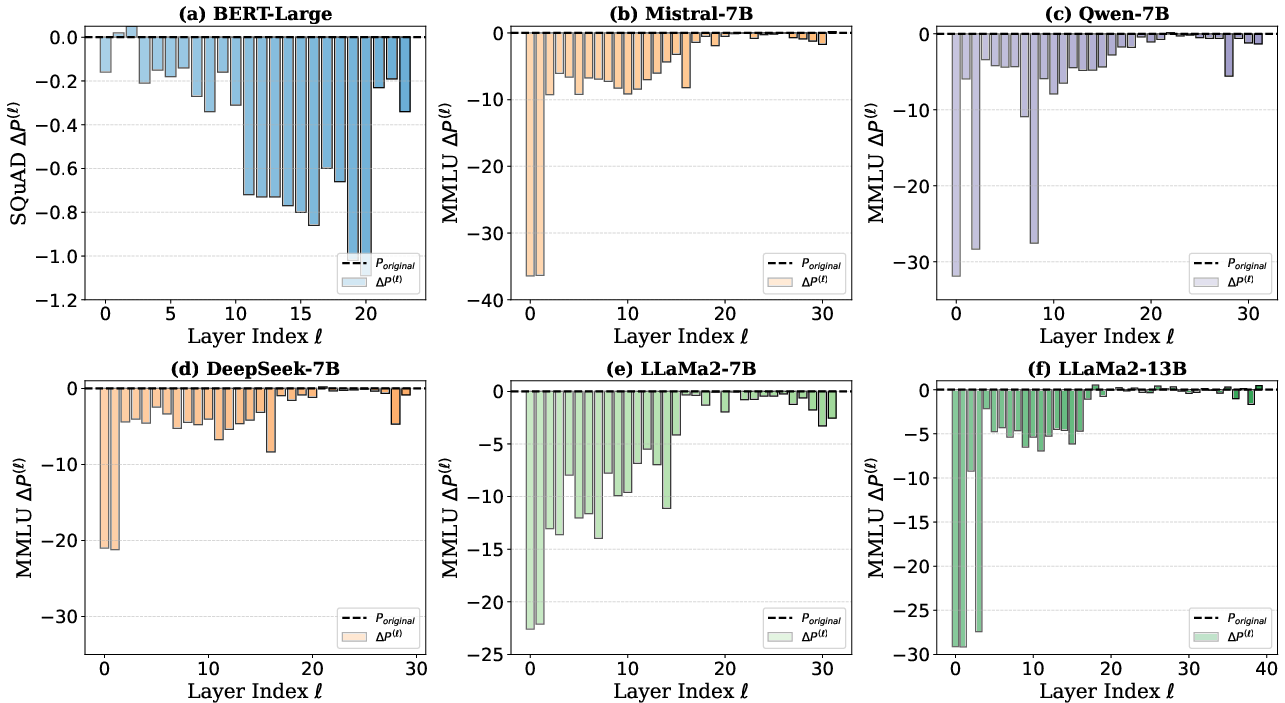
Figure 1: Performance drop of layer pruning across different LLMs demonstrating significant inefficiency in deeper layers for Pre-LN models.

Theoretical Analysis and Root Cause Identification

The theoretical underpinning of CoD is rooted in the behavior of Pre-LN, which normalizes inputs before applying transformations, resulting in exponential accumulation of output variance as depth increases. This positions derivatives of deeper Pre-LN layers close to the identity matrix, stagnating their transformative capacity. Analyzing variance growth in the LLaM-130M model reinforces this behavior, showing exponential variance amplification irrespective of training progress (Figure 2).

Figure 2: Variance growth across layers in LLaMA-130M with Pre-LN, indicating uncontrolled variance amplification as depth increases.

LayerNorm Scaling: A Mitigation Strategy

To counteract the CoD, the paper proposes LayerNorm Scaling, a novel adjustment to the normalization process that scales the output inversely with the square root of the layer index. This modification effectively curtails variance growth, stabilizing the training dynamics and enhancing the contribution of deeper layers. A comparative analysis between Pre-LN and LayerNorm Scaling illustrates the effectiveness of this approach in controlling variance across layers (Figure 3).

Figure 3: Layerwise output variance comparison, showcasing the efficacy of LayerNorm Scaling in controlling variance across layers.

Experimental Validation

Extensive experiments spanning various model sizes (130M to 1B parameters) validate LayerNorm Scaling's superior performance in both LLM pre-training and downstream task performance. Notably, models using LayerNorm Scaling consistently outperform those using standard normalization techniques in terms of perplexity and task accuracy. For instance, significant improvements in representation learning efficacy and task performance were observed in fine-tuning tasks like MMLU and ARC-e benchmarks (Table \ref{tab:model_comparison}).

Limitations and Practical Implications

While LayerNorm Scaling addresses and mitigates the variance amplification issue effectively, its implementation should consider specific architectural and training contexts. It introduces no additional hyperparameter tuning, simplifying adoption in existing frameworks. This work highlights the critical need for reconsidering deep LLM layer contributions and resource allocations. Its practical implications suggest a more resource-efficient and environmentally sustainable approach to training large-scale LLMs.

Conclusion

The "Curse of Depth in LLMs" presents a critical evaluation of modern LLM architectures, identifying variance amplification as a core issue restricting deep layer utility. By examining this phenomenon across different models and proposing LayerNorm Scaling, the paper offers a promising pathway to enhancing deep layer effectiveness and model performance, thereby fostering more efficient AI resource utilization.