Transformer-Squared: Self-adaptive LLMs

Abstract: Self-adaptive LLMs aim to solve the challenges posed by traditional fine-tuning methods, which are often computationally intensive and static in their ability to handle diverse tasks. We introduce Transformer-Squared, a novel self-adaptation framework that adapts LLMs for unseen tasks in real-time by selectively adjusting only the singular components of their weight matrices. During inference, Transformer-Squared employs a two-pass mechanism: first, a dispatch system identifies the task properties, and then task-specific 'expert' vectors, trained using reinforcement learning, are dynamically mixed to obtain targeted behavior for the incoming prompt. Our method consistently outperforms ubiquitous approaches such as LoRA, with fewer parameters and greater efficiency. Furthermore, Transformer-Squared demonstrates versatility across different LLM architectures and modalities, including vision-language tasks. Transformer-Squared represents a significant leap forward, offering a scalable, efficient solution for enhancing the adaptability and task-specific performance of LLMs, paving the way for truly dynamic, self-organizing AI systems.

• The paper's main contribution is introducing Singular Value Fine-tuning (SVF) for parameter-efficient LLM adaptation via reinforcement learning.
• It demonstrates consistent performance gains and reduced parameter overhead, outperforming LoRA in both domain-specific and out-of-distribution tasks.
• The framework enables dynamic composition of expert modules, ensuring robust, scalable adaptation and cross-architecture transferability.

Self-Adaptive LLMs via Singular Value Fine-Tuning

Introduction

The paper "Transformer-Squared: Self-adaptive LLMs" (2501.06252) presents a parameter-efficient adaptation framework for LLMs based on Singular Value Fine-tuning (SVF) and reinforcement learning (RL). Traditional post-training and fine-tuning methodologies for LLMs are computationally demanding and statically optimize model behavior for specific tasks or broad task categories. This often leads to performance trade-offs, rigidity, and increased susceptibility to overfitting, especially with narrow or small datasets. The work motivates a self-adaptive paradigm where expert modules, each targeting particular domains or skills, can be dynamically composed during inference to adapt LLMs for arbitrary downstream tasks.

The central contributions are the introduction of SVF as a new PEFT technique and the design of the Transformer self-adaptation framework, which combines pre-trained expert vectors in real time via a two-pass inference mechanism. Experimental results demonstrate consistent performance improvements over LoRA and other PEFT baselines, scalability across multiple LLM architectures and modalities, and applicability to both established and out-of-distribution tasks.

Methodology

Singular Value Fine-tuning (SVF)

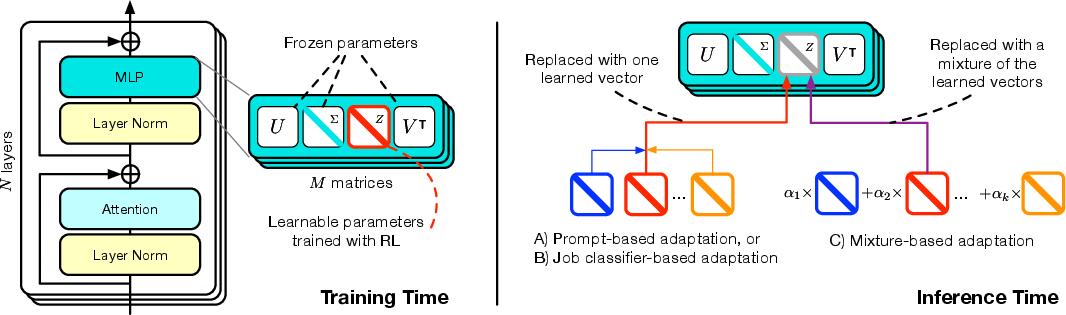
SVF restricts adaptation to scaling the singular values of each weight matrix in the transformer stack. Given a weight matrix $W = U\Sigma V^\intercal$, the method introduces a scaling vector $z$ such that the fine-tuned matrix becomes $$W' = U(\Sigma \otimes \operatorname{diag}(z))V^\intercal$$. Each $z$ is trained via RL (using the REINFORCE algorithm), directly optimizing end-task reward with KL regularization to penalize divergence from the original model policy. This design has several technical advantages:

• Parameter efficiency: Only $r \leq \min(m, n)$ parameters are introduced per matrix, where $r$ is the rank, often resulting in orders of magnitude lower overhead than LoRA, especially at typical LoRA ranks.
• Compositionality: The axes of modification (singular vectors) are independent and interpretable, enabling straightforward and theoretically faithful composition or interpolation of expert skill vectors.
• Regularization: Changes are constrained strictly to the latent semantic axes already embedded in the pretrained weight manifolds, mitigating overfitting and catastrophic forgetting.

Self-Adaptation Framework

The Transformer self-adaptive mechanism functions as follows:

• Expert Collection (training): For each target domain or task, an SVF vector is trained to specialize the base LLM towards that domain using small RL-optimized datasets.
• Inference (two-pass): Upon receiving a prompt, a dispatch/identification step determines which expert or mixture of experts is most suited. The selected adaptation is then applied as a singular value transformation, and the response is generated on the adjusted model.

Three adaptation strategies are formalized:

• Prompt Engineering: The LLM is prompted to classify/detect the task domain, mapping directly to a corresponding expert vector.
• Classification Expert: An SVF-trained classifier head determines the optimal expert adaptation.
• Few-shot CEM Adaptation: A small pool of task examples is used with cross-entropy method (CEM) optimization to search for the best convex combination of experts, maximizing performance for the new domain via elite sampling.

  Figure 1: Method overview of SVF-based expert extraction (left) and the adaptive combination mechanism at inference (right).

Empirical Results

Performance Across Domains and Models

Extensive experiments were conducted on Llama3-8B-Instruct, Mistral-7B-Instruct-v0.3, and Llama3-70B-Instruct base models. SVF outperformed LoRA and other baselines (e.g., IA3, DORA) across core benchmarks (GSM8K, MBPP-Pro, ARC-Easy) in both direct fine-tuning and self-adaptive transfer scenarios. Notable quantitative findings include:

• Parameter reduction: SVF consistently achieved superior or competitive results with less than 10% of LoRA's parameter overhead.
• Generalization: SVF enabled effective adaptation to out-of-distribution tasks (e.g., MATH, ARC-Challenge, Humaneval, and even vision-language OKVQA) using only language-trained experts.
• Robust learning curves: SVF showed stable and monotonic validation improvements without the collapse and instability frequently observed in RL-trained LoRA regimes.

  Figure 2: SVF fine-tuning learning curves for diverse tasks, illustrating rapid convergence and stable performance gains over the base model.

Strong empirical performance is particularly evident when comparing normalization scores for domain-specific and transfer tasks. For example, SVF improved Llama3-8B-Instruct's test accuracy on GSM8K to 79.15 (from 75.89 base, relative score 1.04). In out-of-domain adaptation, Transformer (few-shot) achieved higher normalized scores on MATH (1.04), ARC-Challenge (1.02), and Humaneval (1.03) than both the static model and LoRA baseline.

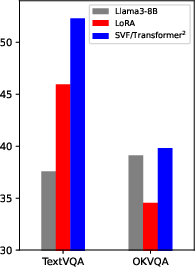
Figure 3: SVF improves LLM base test scores and offers competitive performance for both language and VLM domains.

Adaptation Scalability and Strategy Ablation

• Dispatch Precision: Confusion matrices demonstrate high task-recognition accuracy for both prompt and classification expert methods—misclassification rates remain low, and adaptation strategies benefit from improved task identification.
• Adaptation Mix: Few-shot CEM mixtures leverage expert specialization, with domain-relevant experts receiving highest interpolation weights on aligned tasks, though nontrivial contributions from orthogonal experts are commonplace, highlighting compositionality.
• Cross-model/reuse: SVF expert vectors, when applied to other models of similar architecture (e.g., Llama3-8B-Instruct SVFs adapted to Mistral-7B-Instruct-v0.3), yield positive transfer in several tasks. This demonstrates nontrivial alignment between singular vector parametrizations across architectures.

  Figure 4: Confusion matrices for expert selection strategies, indicating robust classification accuracy.

  

  Figure 5: PCA on Llama3-8B-Instruct weight matrices; low-rank approaches do not capture sufficient information for compositional adaptation.

  

  Figure 6: PCA on Mistral-7B-Instruct-v0.3 reveals similarly broad singular-value spectra outside self-attention QKV, motivating full-rank SVF approaches.

Efficiency and Practicality

• Inference Overhead: The self-adaptive framework introduces an additional inference pass; in practice, for multi-turn tasks, this overhead is amortized and generally moderate (e.g., 13–47% of solve time, depending on prompt/task length).
• Few-shot adaptation: Performance plateaus with as few as 3–5 held-out task examples for CEM adaptation, underscoring sample efficiency and suitability for low-resource domains.

Implications and Future Directions

Practical implications: Transformer enables efficient deployment and continual improvement of LLMs in lifelong or production environments, supporting rapid adaptation to emerging domains or user needs without retraining large networks. The architecturally agnostic and highly compositional nature of SVF encourages transfer learning, model merging, and modular skill deployment.

Theoretical implications: By restricting adaptation to scaling existing singular axes, SVF advances parameter-efficient fine-tuning, bridges with subspace regularization, and suggests a framework for controllable model composition. The empirical cross-model transferability of SVF vectors hints at shared latent structure among model families.

Future developments: Model merging techniques, more nuanced inference-time adaptation policies, and extension to radically different architectures (e.g., multimodal transformers beyond V+L) represent promising research avenues. Efficient optimization methods for online adaptation—in particular, for high-dimensional interpolation—also remain open.

Conclusion

"Transformer-Squared: Self-adaptive LLMs" introduces a theoretically grounded and practically effective approach to self-adaptive language modeling. SVF redefines the parameter-efficient fine-tuning landscape, offering compositional adaptation, regularization, and scalability, while the modular Transformer framework advances LLMs toward lifelong adaptability and dynamic skill composition. These findings suggest a productive direction for building AI systems capable of real-time, expert-informed adaptation, with broad implications in deployment, sustainability, and cross-architecture transfer.