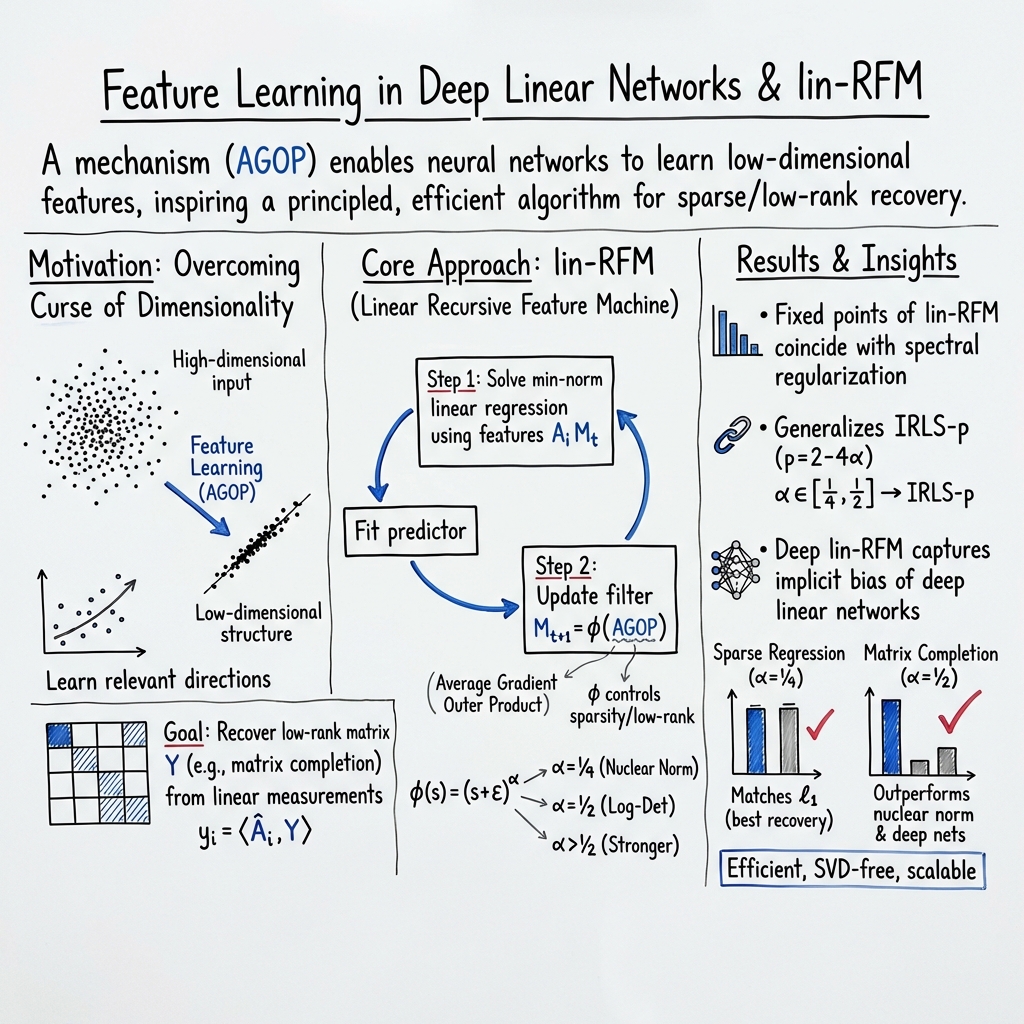
Linear Recursive Feature Machines provably recover low-rank matrices (2401.04553v1)

Abstract: A fundamental problem in machine learning is to understand how neural networks make accurate predictions, while seemingly bypassing the curse of dimensionality. A possible explanation is that common training algorithms for neural networks implicitly perform dimensionality reduction - a process called feature learning. Recent work posited that the effects of feature learning can be elicited from a classical statistical estimator called the average gradient outer product (AGOP). The authors proposed Recursive Feature Machines (RFMs) as an algorithm that explicitly performs feature learning by alternating between (1) reweighting the feature vectors by the AGOP and (2) learning the prediction function in the transformed space. In this work, we develop the first theoretical guarantees for how RFM performs dimensionality reduction by focusing on the class of overparametrized problems arising in sparse linear regression and low-rank matrix recovery. Specifically, we show that RFM restricted to linear models (lin-RFM) generalizes the well-studied Iteratively Reweighted Least Squares (IRLS) algorithm. Our results shed light on the connection between feature learning in neural networks and classical sparse recovery algorithms. In addition, we provide an implementation of lin-RFM that scales to matrices with millions of missing entries. Our implementation is faster than the standard IRLS algorithm as it is SVD-free. It also outperforms deep linear networks for sparse linear regression and low-rank matrix completion.