- The paper introduces Logic-LM, a framework that integrates LLMs with symbolic solvers to enhance logical reasoning.
- It employs a three-module design for problem formulation, symbolic reasoning, and result interpretation, achieving up to 39.2% improvement over standard prompting on complex tasks.
- The study demonstrates that self-refinement based on solver feedback increases symbolic accuracy and overall model robustness in diverse logical reasoning scenarios.
Logic-LM: Integrating LLMs with Symbolic Solvers
The paper proposes a framework named Logic-LM, designed to enhance the logical reasoning capabilities of LLMs by integrating symbolic solvers. This approach aims to overcome LLMs' struggles with complex logical problems by leveraging symbolic inference engines to ensure reasoning faithfulness and transparency. The framework includes a novel self-refinement module to ensure accurate symbolic formalizations, using feedback from symbolic solvers to iteratively refine logical representations.
Framework Overview
Logic-LM consists of three key modules: the Problem Formulator, the Symbolic Reasoner, and the Result Interpreter.
- Problem Formulator: This module utilizes LLMs to translate natural language problems into symbolic representations. By defining a task-specific grammar for logic programming (LP), first-order logic (FOL), constraint satisfaction problems (CSP), and boolean satisfiability (SAT) formulations, the Problem Formulator creates symbolic statements that serve as inputs for symbolic solvers.
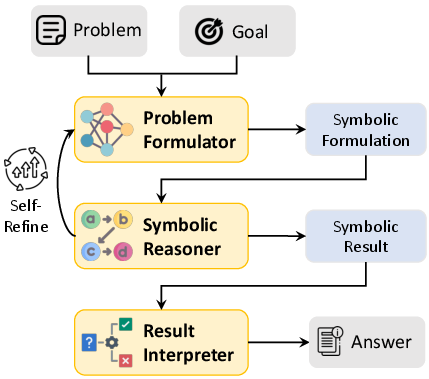 *Figure 1: Overview of our Logic-LM framework. *
*Figure 1: Overview of our Logic-LM framework. *
- Symbolic Reasoner: This component uses external deterministic solvers tailored to specific reasoning tasks—LP systems for deductive reasoning, Prover9 for FOL, python-constraint for CSP, and Z3 for SAT—to infer solutions or prove propositions based on the given symbolic input.
- Result Interpreter: This module translates solver results back into natural language answers. Depending on the problem's complexity, it employs either rule-based or LLM-based methods to perform this translation.
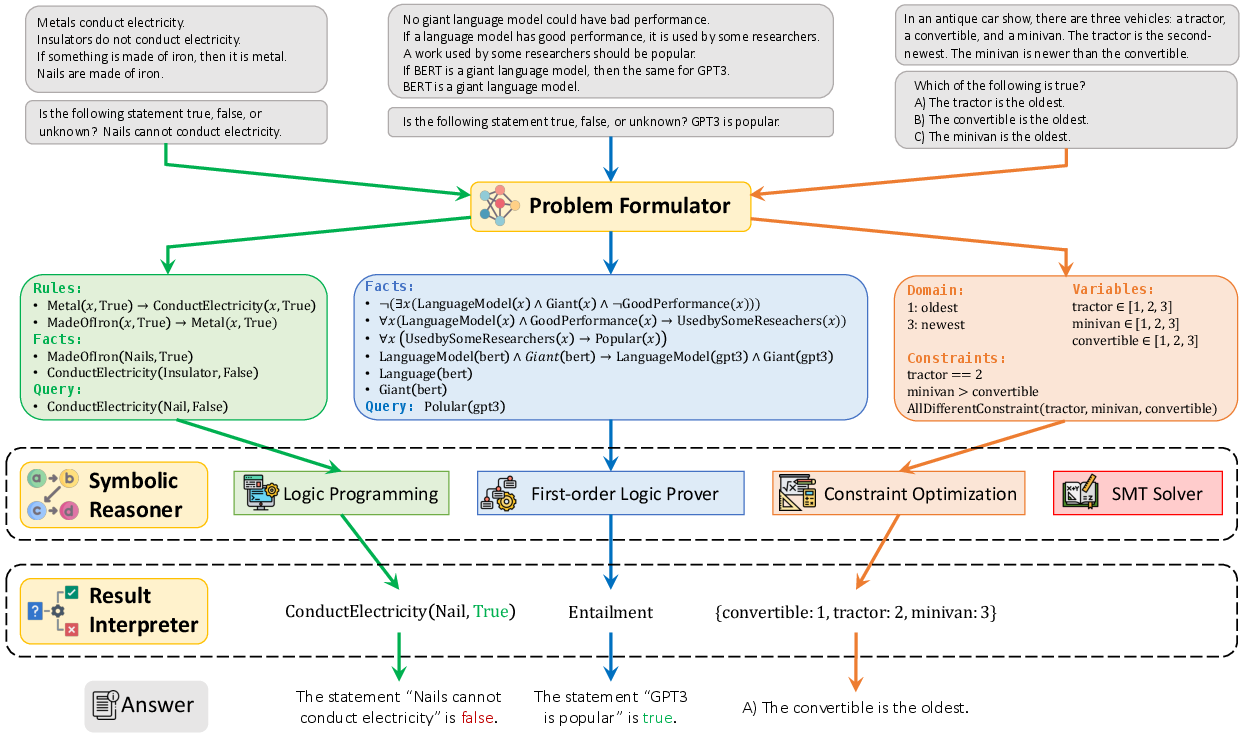
Figure 2: Overview of our Logic-LM model, which consists of three modules: (1)~Problem Formulator generates a symbolic representation for the input problem with LLMs via in-context learning (2)~Symbolic Reasoner performs logical inference on the formulated problem, and (3)~Result Interpreter interprets the symbolic answer.
Experimental Setup
The paper evaluates Logic-LM's effectiveness across five logical reasoning datasets: ProofWriter, PrOntoQA, FOLIO, LogicalDeduction, and AR-LSAT. These datasets encompass various logical reasoning tasks, including deductive reasoning, first-order logic reasoning, constraint satisfaction problems, and analytical reasoning. Logic-LM's performance is compared against standard prompting and chain-of-thought prompting methods, using models such as ChatGPT and GPT-4 for the underlying LLMs.
Results and Observations
- Performance Enhancement: Logic-LM significantly enhances performance over standard LLM prompting and chain-of-thought prompting. On average, it achieves a 39.2% improvement over standard prompting and an 18.4% improvement over chain-of-thought prompting, highlighting the robustness of integrating symbolic solvers.
- Reasoning Depth and Robustness: The effectiveness of Logic-LM grows with the complexity of the reasoning task, particularly when the required reasoning depth increases. Its ability to delegate complex reasoning to symbolic solvers ensures faithfulness and robustness that purely language-based methods lack, especially evident on more complex datasets such as FOLIO.
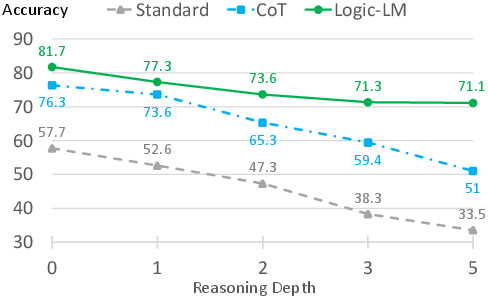
Figure 3: Accuracy of different models for increasing size of reasoning depth on the ProofWriter dataset.
- Self-Refinement Impact: Introducing self-refinement improves the accuracy of symbolic formulations by iteratively refining the logic representation based on solver feedback. This process increases executable rates and enhances overall model performance.
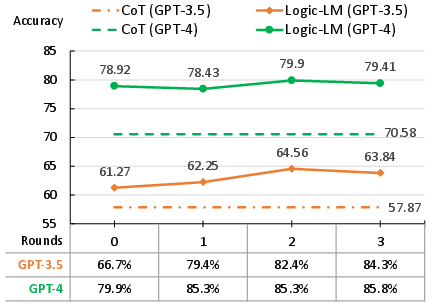
Figure 4: The accuracy for different rounds of self-refinement, with the corresponding executable rates.
Case Studies
In examining specific examples, the paper showcases Logic-LM's symbolic generation capabilities and some persistent challenges, such as accurately defining predicates and handling natural language ambiguity. These examples demonstrate areas for improvement and potential further refinements.

Figure 5: An example of the generated symbolic representation and the predicted answer by Logic-LM.
Conclusion
Logic-LM represents a promising approach to improving logical reasoning in LLMs by combining the interpretability of symbolic solvers with the robust language understanding capabilities of modern LLMs. Future advancements could include more adaptable logic systems, such as probabilistic soft logic, to address reasoning in contexts of uncertainty and commonsense challenges.
 *Figure 1: Overview of our
*Figure 1: Overview of our 


