- The paper demonstrates that real-world datasets are compressible, contradicting the NFL theorem’s implications.
- It reveals that neural networks favor low-complexity solutions, validating a simplicity bias in supervised learning tasks.
- Findings imply that unified models with soft inductive biases can generalize effectively across varied domains.
The No Free Lunch Theorem, Kolmogorov Complexity, and the Role of Inductive Biases in Machine Learning
Introduction
The paper "The No Free Lunch Theorem, Kolmogorov Complexity, and the Role of Inductive Biases in Machine Learning" investigates the implications of the No Free Lunch (NFL) theorem within the context of supervised learning and explores the role of inductive biases and Kolmogorov complexity in machine learning. The authors argue that contrary to the NFL theorem, which suggests that every learner achieves the same average performance across all possible problems, real-world datasets are not uniformly distributed but rather exhibit lower complexity. This preference for low complexity is reflected in both the data and the learning models used to process them.
Figure 1: Over time, tasks that were performed by domain-specialized ML systems are increasingly performed by unified neural network architectures.
Kolmogorov Complexity and Dataset Compressibility
The paper explores Kolmogorov complexity as a measure of the structural simplicity of datasets. Kolmogorov complexity is defined as the length of the shortest program that can produce a given output in a fixed programming language. A significant finding is that real-world datasets are compressible, highlighting that these datasets exhibit low complexity. For example, text and audio datasets, when subject to compression algorithms, yielded much smaller sizes than would be expected under uniform distribution, demonstrating observable structure in the data.
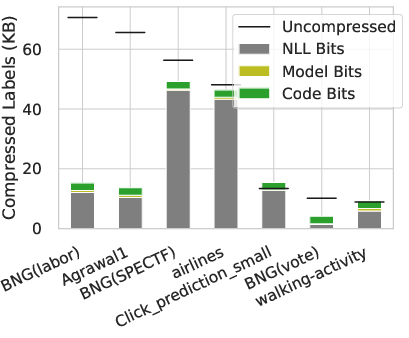
Figure 2: (Left): Compressed sizes of tabular labels where compression is performed via a trained MLP model.
Neural Networks and Simplicity Bias
The study further articulates that neural networks inherently prefer solutions with lower Kolmogorov complexity. This simplicity bias suggests that even randomly initialized models like GPT-2 prioritize simpler sequence completions, aligning well with similar biases observed in real-world data. Complex datasets that are uniformly sampled are exponentially unlikely to occur, thus validating the use of general models that favor low complexity to solve real-world problems efficiently.
Cross-Domain Generalization and Model Selection
An essential contribution of the paper is demonstrating that neural networks, particularly CNNs, can generalize well across unrelated domains, such as tabular datasets, due to their simplicity bias. The authors also challenge the prevailing perception that small datasets require small, constrained models, positing instead that a single flexible learner with a simplicity bias can perform well across both small and large datasets.


Figure 3: GPT-3 prefers low-complexity sequences generated by expression trees.
Implications and Future Directions
The implications of this research are significant for the design of general-purpose models in AI. By favoring soft inductive biases that allow flexibility within models rather than imposing restrictive constraints, this approach encourages the development of models that can handle a wide range of tasks. The paper pushes back against the NFL theorem's narrative by highlighting that structured real-world data enable the use of unified models for diverse applications, further supported by the alignment of neural network biases with data complexities.
In conclusion, this paper provides a comprehensive understanding of how simplicity biases and Kolmogorov complexity contribute to the success of machine learning models, and suggests that embracing these concepts can lead to the development of more robust and versatile AI systems.



