Optimal compression of quantum many-body time evolution operators into brickwall circuits

Abstract: Near term quantum computers suffer from a degree of decoherence which is prohibitive for high fidelity simulations with deep circuits. An economical use of circuit depth is therefore paramount. For digital quantum simulation of quantum many-body systems, real time evolution is typically achieved by a Trotter decomposition of the time evolution operator into circuits consisting only of two qubit gates. To match the geometry of the physical system and the CNOT connectivity of the quantum processor, additional SWAP gates are needed. We show that optimal fidelity, beyond what is achievable by simple Trotter decompositions for a fixed gate count, can be obtained by compiling the evolution operator into optimal brickwall circuits for the $S = 1/2$ quantum Heisenberg model on chains and ladders, when mapped to one dimensional quantum processors without the need of additional SWAP gates.

• The paper introduces a method to compress quantum many-body time evolution operators into shallow brickwall circuits that maintain fidelity without extra SWAP gates.
• It employs Trotter decomposition and gate parameterization techniques optimized through tensor network methods and operator entanglement entropy.
• Simulations demonstrate that the optimized circuits deliver superior fidelity and resource efficiency for spin-1/2 Heisenberg models across different lattice geometries.

Optimal Compression of Quantum Many-Body Time Evolution Operators into Brickwall Circuits

Introduction

The paper addresses the challenge of efficiently simulating quantum many-body systems on near-term quantum computers. Given the constraints of decoherence and limited circuit depth in quantum hardware, the authors propose a methodology to achieve high-fidelity simulations using brickwall circuits optimized for quantum processors lacking extensive connectivity. The focus is on compressing time evolution operators into shallow brickwall circuits that maintain fidelity without introducing additional SWAP gates, specifically for the $S=1/2$ quantum Heisenberg model.

Figure 1: The chain (left) and triangular ladder (right) lattice geometries used in this work.

Model and Methodology

The study employs lattice models of spin-$1/2$ systems with SU(2) symmetric Heisenberg interactions to explore the effectiveness of brickwall circuit architectures. Two distinct geometries are analyzed: a linear chain and a triangular ladder, mapped to quantum processors configured in a one-dimensional array. The time evolution operator $\mathcal{U}(t)=\exp(-itH)$ is decomposed into gates using Trotter methods, and further optimized through parametric variations into brickwall layouts optimized classically.

Figure 2: Left: A brickwall circuit with depth $M=2$ for six qubits, with each color representing an $M=1$ layer. Right: Parametrization of a two-qubit unitary as a product of four single qubit gates and one two-qubit gate.

Gate Optimization

Optimizing gate configurations within brickwall circuits involves mapping two-qubit unitary operations to a series of parametrized single and two-qubit gates, minimizing infidelity against an ideal time evolution operator. Effective parameter optimization demands consideration of gauge freedom between circuit layers and employs tensor network methods for computational efficiency. The operator entanglement entropy (opEE) serves as a metric for measuring gate efficacy in circuit compression.

Figure 3: Left: The blue brickwall layer encodes the first-order Trotter decomposition for NN interacting Hamiltonians. Right: The decomposition involving SWAP gates, used to convert the NNN two-qubit gate into circuits with only NN gates.

Results and Analysis

Extensive simulations indicate that the optimal brickwall circuits exhibit superior fidelity relative to traditional Trotter circuits per gate count. Parameterization of gates shows diversity within opEE distributions, suggesting embedded configurations reminiscent of swap operations. Furthermore, the ability of brickwall circuits to propagate time evolution operators robustly across lattice geometries speaks to their advantageous application in fidelities and out-of-time-ordered correlators (OTOCs).

Figure 4: The gauge freedom that exists between the layers of a circuit.

Conclusions and Implications

The development of brickwall circuits tailored to the constraints of quantum architectures marks a significant step toward cost-effective digital quantum simulation. The proposed methodologies demonstrate potential scalability and adaptability in simulating systems with non-standard connectivity, reducing resource demands particularly concerning gate counts and decoherence impacts. The techniques outlined stand to influence future quantum simulation strategies, emphasizing an evolved approach to circuit construction and optimization.

Future Directions

The adaptation of symmetry constraints at the gate level presents a promising avenue to further streamline circuit architectures. Enhancements in noise modeling and the exploration of varied optimization cost functions can deepen the applicability of brickwall configurations across different quantum domains. This foundational work invites continued exploration into the symmetries and efficiencies inherent in quantum many-body simulation methodologies.

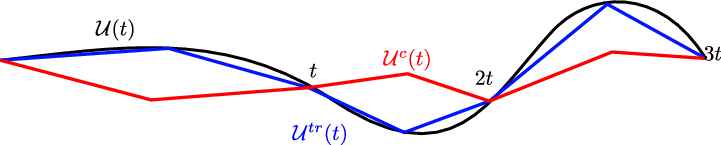
Figure 5: A sketch of the "refocussing" mechanism that potentially explains the structures observed in refocusing behaviors.