AutoSDF: Shape Priors for 3D Completion, Reconstruction and Generation

Abstract: Powerful priors allow us to perform inference with insufficient information. In this paper, we propose an autoregressive prior for 3D shapes to solve multimodal 3D tasks such as shape completion, reconstruction, and generation. We model the distribution over 3D shapes as a non-sequential autoregressive distribution over a discretized, low-dimensional, symbolic grid-like latent representation of 3D shapes. This enables us to represent distributions over 3D shapes conditioned on information from an arbitrary set of spatially anchored query locations and thus perform shape completion in such arbitrary settings (e.g., generating a complete chair given only a view of the back leg). We also show that the learned autoregressive prior can be leveraged for conditional tasks such as single-view reconstruction and language-based generation. This is achieved by learning task-specific naive conditionals which can be approximated by light-weight models trained on minimal paired data. We validate the effectiveness of the proposed method using both quantitative and qualitative evaluation and show that the proposed method outperforms the specialized state-of-the-art methods trained for individual tasks. The project page with code and video visualizations can be found at https://yccyenchicheng.github.io/AutoSDF/.

• The paper introduces a unified framework with patchwise VQ-VAE encoding and a non-sequential transformer prior for diverse 3D shape synthesis from partial inputs.
• It achieves superior results in shape completion, single-view reconstruction, and language-guided generation by lowering Unrealized Hausdorff Distance and raising Total Mutual Difference.
• The approach reduces annotation costs and supports efficient, multimodal inference, opening promising avenues for robotics, augmented reality, and flexible 3D modeling.

AutoSDF: Non-sequential Autoregressive Shape Priors for Multimodal 3D Synthesis

Introduction

"AutoSDF: Shape Priors for 3D Completion, Reconstruction, and Generation" (2203.09516) introduces a unified framework for multimodal 3D generative modeling leveraging a non-sequential autoregressive shape prior. The methodology enables high-fidelity, diverse 3D shape synthesis from partial observations, images, and language descriptions, outperforming domain-specific baselines across shape completion, single-view reconstruction, and text-guided generation tasks. This work is characterized by a structured compositional approach: a VQ-VAE-based discretization of shapes, patch-wise latent encoding for local independence, and a transformer that models the prior over arbitrary latent subsets, enabling efficient, scalable inference with minimal paired supervision.

Methodology

The framework proceeds as follows:

1. 3D Shape Discretization: A 3D VQ-VAE encodes volumetric Truncated Signed Distance Fields (T-SDFs) of shapes into a patch-wise, low-dimensional, discrete latent grid. This patchwise encoding enforces locality, mitigating the entanglement of global context in the latent variables and ensuring correspondence between partial observations in the shape and those in the latent space.

   Figure 1: AutoSDF pipeline—VQ-VAE patch-wise encoding produces local discrete latents, enabling the downstream transformer prior to support arbitrary spatial conditioning and non-sequential inference.

2. Non-sequential Autoregressive Prior: A transformer is trained to model $p(\mathbf{Z})$, where $\mathbf{Z}$ is a discrete latent grid representing the shape, using randomized sampling orders. For any arbitrary subset of revealed latent variables, the transformer models the distribution over the remainder, supporting conditioning on arbitrary spatial observations, unlike classical autoregressive models with fixed orderings.
3. Task-specific Conditionals and Product Inference: For conditional generation, lightweight domain-specific encoders (e.g., CNNs for images, BERT for text) predict independent per-location distributions over latent variables ("naive conditionals") given the conditioning input. At inference, the transformer prior and naive conditionals are combined multiplicatively across the latent grid, yielding a posterior over shapes consistent with both the prior and conditioning signal.

   Figure 2: Conditional generation—domain and modality-specific encoders are paired with the learned prior for product inference across partial input types.

Experimental Results

Multimodal Shape Completion

The model is evaluated on ShapeNet for partial-to-full shape completion, with the input comprising visible subregions (e.g., bottom half, arbitrary octants). Compared to point cloud-based state-of-the-art methods such as MPC and PoinTr, AutoSDF delivers stronger fidelity-diversity tradeoffs—lower Unidirectional Hausdorff Distance (UHD) and higher Total Mutual Difference (TMD), particularly preserving the structure and diversity from partial cues.

Figure 3: Shape completion—AutoSDF completions from partial input retain the geometry of visible legs or other features, unlike baselines which may oversmooth or ignore cues.

Figure 4: Qualitative diversity—AutoSDF samples represent diverse but plausible completions even with highly sparse initial observations.

Single-view 3D Reconstruction

On both ShapeNet and Pix3D, AutoSDF is trained with minimal (image, shape) pairs, outperforming approaches such as Pix2Vox, ResNet2TSDF, and direct latent prediction baselines. The model yields higher IoU, lower Chamfer Distance, and higher F-score, crucially generating multiple plausible shapes for ambiguous inputs (e.g., images captured from a single viewpoint, occluding parts of the geometry).

Figure 5: Single image to multiple plausible 3D reconstructions. Shape diversity in unseen regions demonstrates the expressivity of the prior-modality product.

Language-guided Generation

The model synthesizes 3D shapes conditioned on natural language using the ShapeGlot dataset. Against Text2Shape (T2S) and a transformer joint-encoder baseline (JE), AutoSDF achieves higher preference scores in evaluator studies (e.g., 66% vs 18% for T2S), and produces outputs that align well with both specific and open-ended descriptions, capturing both specificity and diversity.

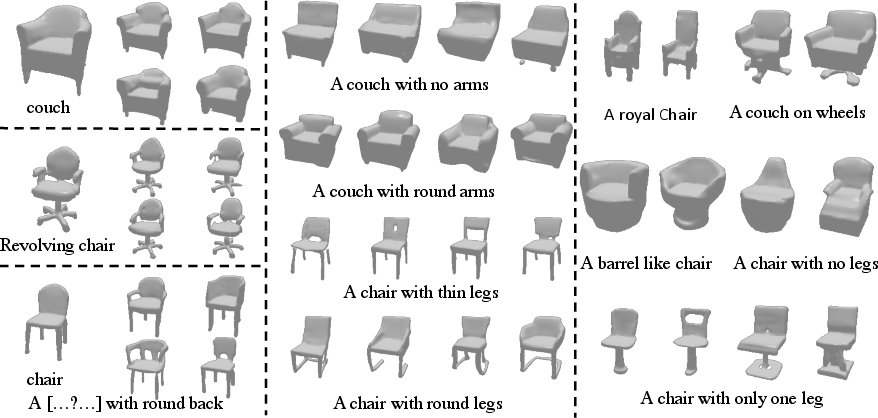
Figure 6: Natural language conditioning—"a chair with one leg" leads to coherent and plausible samples appropriately matching the conditioning phrase.

Ablations and Qualitative Analyses

Further analyses highlight:

• The role of patchwise independence—crucial for mapping observations to latent conditionals.
• The impact of prior versus conditional weighting in product inference, which dictates the balance between shape plausibility and faithfulness to the conditioning signal.
• Extensive qualitative results demonstrate generalization, modality alignment, and realistic sample diversity across domains.

  Figure 7: Unconditional transformer generation samples—demonstrating broad coverage over generic shape classes in ShapeNet.

  

  Figure 8: Additional shape completion comparisons with baseline models.

  

  Figure 9: Comparison in language-conditioned generation to baselines demonstrating higher condition-faithfulness and shape validity.

Implications and Future Directions

AutoSDF operationalizes the notion that a composable, expressive shape prior—when properly disentangled from task-specific conditionals—serves as a foundation for robust multimodal 3D generation. This supports efficient transfer to new tasks with limited paired data, modularity across modalities, and the generation of diverse outputs reflective of posterior uncertainty.

Key implications and considerations include:

• Task-agnostic priors reduce annotation costs and better capture shape variation, aiding robotics and AR pipelines requiring flexible inference from incomplete and multimodal signals.
• Product-based inference trades modeling optimality for tractability; if paired data is abundant, joint modeling could be explored, but in many real-world cases, the proposed factorization is advantageous.
• Limitations: The approach is currently tailored to spatially-aligned voxel/TSDF representations and may not trivially extend to unstructured meshes or implicit neural representations. Also, the learned priors are only as diverse as the underlying 3D datasets (primarily ShapeNet CAD models).

The extension of the compositional prior framework to alternative 3D parameterizations (e.g., meshes, point clouds, neural implicits) and the integration with downstream manipulation and robotic perception tasks present promising avenues for future investigation.

Conclusion

AutoSDF introduces a non-sequential transformer-based autoregressive prior over discretized 3D shape latents, enabling unified, multimodal shape completion and generation with superior diversity, faithfulness, and generalization across modalities. The approach advances the modeling of uncertainty in 3D inference tasks, offering a flexible and composable architecture that is competitive across diverse benchmarks and input conditions.