Checkmate: Breaking the Memory Wall with Optimal Tensor Rematerialization

Abstract: We formalize the problem of trading-off DNN training time and memory requirements as the tensor rematerialization optimization problem, a generalization of prior checkpointing strategies. We introduce Checkmate, a system that solves for optimal rematerialization schedules in reasonable times (under an hour) using off-the-shelf MILP solvers or near-optimal schedules with an approximation algorithm, then uses these schedules to accelerate millions of training iterations. Our method scales to complex, realistic architectures and is hardware-aware through the use of accelerator-specific, profile-based cost models. In addition to reducing training cost, Checkmate enables real-world networks to be trained with up to 5.1x larger input sizes. Checkmate is an open-source project, available at https://github.com/parasj/checkmate.

• The paper introduces Checkmate for efficient tensor rematerialization to trade recomputation for memory savings during DNN training.
• It formulates the rematerialization problem as an ILP and employs a two-phase rounding strategy to approximate optimal schedules.
• Experiments show up to 5.1× larger feasible input sizes, enabling larger batch sizes and complex model exploration.

Checkmate: Breaking the Memory Wall with Optimal Tensor Rematerialization

The paper "Checkmate: Breaking the Memory Wall with Optimal Tensor Rematerialization" introduces Checkmate, a system aimed at efficiently rematerializing deep neural networks (DNNs) to optimize memory usage during training without incurring excessive computational overhead. This approach focuses on overcoming limitations posed by the memory capacity of hardware accelerators such as GPUs. The contributions include a detailed formalization of tensor rematerialization, an integer linear programming (ILP) based approach to determine optimal schedules, and a polynomial-time approximation strategy for practical applicability in real-world scenarios.

Problem Statement and Motivation

Increasingly larger models and datasets in deep learning have resulted in a significant demand for memory during DNN training. Typically, the dominating factor in memory usage is the requirement to store intermediate activation tensors needed for backpropagation. Given the constrained memory capacity of even the most advanced accelerators, this limitation creates a bottleneck in exploring novel architectures that require more resources.

The problem of memory management during training is addressed by strategically implementing checkpoints where intermediate results are stored or recomputed, reducing active memory usage. The idea of rematerializing necessary tensors allows for the intensification of network execution within available memory resources by computationally trading off some runtime efficiency.

Checkmate System Architecture

The Checkmate framework comprises a series of components designed to establish rematerialization schedules. The system operates by transforming the rematerialization challenge into an optimization problem solved through an ILP. The primary feature of Checkmate is its ability to support non-linear architectures such as those with residual connections, offering a memory-aware and hardware-aware solution.

Figure 1: This 32-layer deep neural network requires 30GB of memory. Rematerializing layers, shown as shaded blue regions, reduces the requirement by 21GB.

Optimization Approach

ILP Formalization

Checkmate formulates the rematerialization as a mixed integer linear program that minimizes the overall computational cost while respecting memory constraints. The ILP framework takes into account the architecture of the DNN, memory costs, and computation costs associated with each layer.

Scheduling and Approximation

Execution schedules are incrementally partitioned into stages, each dictating specific operations, residencies, and recomputations. Furthermore, the study introduces a two-phase rounding strategy that efficiently approximates the optimal schedules derived from the continuous relaxation of the ILP, enabling near-optimal solutions in cases where direct ILP solving is intractable due to scale.

Figure 2: Overview of the Checkmate system.

Evaluation

Trade-offs and Performance

The evaluations demonstrate that the use of Checkmate leads to a substantial decrease in memory usage, with experiments showing up to 5.1× larger input sizes feasible on the same hardware platform compared to standard practices. This performance is achieved with minimal computational overhead as indicated by benchmark results across popular model architectures such as VGG16, U-Net, and MobileNet.

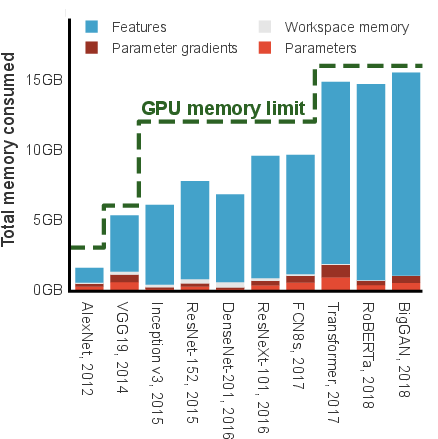
Figure 3: Computational overhead vs. memory budget for several DNNs on NVIDIA V100 GPU.

Practical Implications

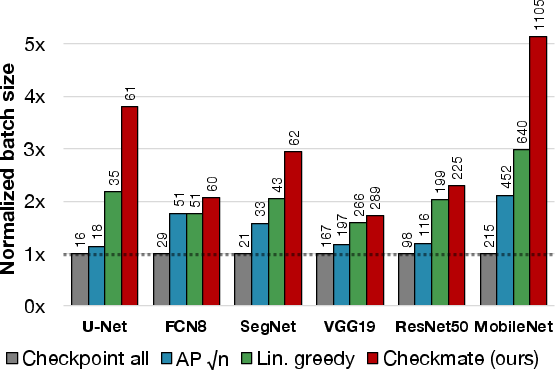
Figure 4: Maximum batch size improvement by Checkmate compared to traditional methods.

Through rigorous testing, Checkmate proves its capability to facilitate larger batch sizes and greater model exploration, paving the way for more sophisticated neural network designs within existing hardware constraints. It highlights how systematic optimization and memory management can help bypass current technological roadblocks set by physical memory limitations.

Conclusion

Checkmate empowers researchers and practitioners by allowing more extensive exploration of model architectures under stringent memory constraints. By integrating hardware-specific profiling and advanced scheduling algorithms, the system not only provides a theoretically sound framework but also a practical tool for real-world deployment. Overall, this technology offers substantial prospects for advancing DNN training efficiency and maximizing the utility of existing computational resources.