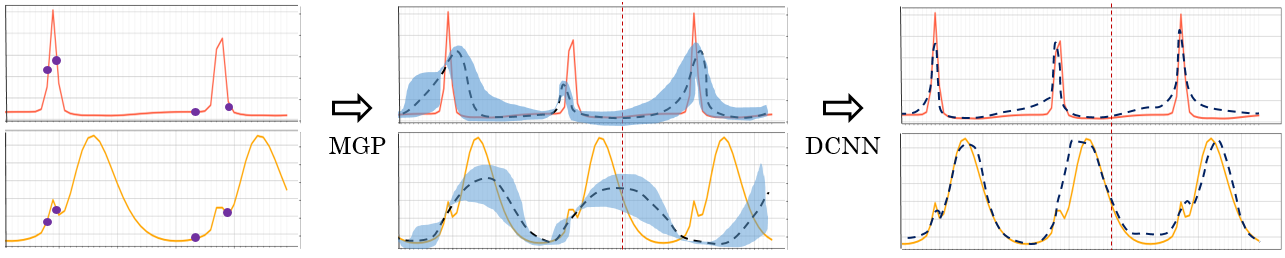
Multi-Task Gaussian Processes and Dilated Convolutional Networks for Reconstruction of Reproductive Hormonal Dynamics
Abstract: We present an end-to-end statistical framework for personalized, accurate, and minimally invasive modeling of female reproductive hormonal patterns. Reconstructing and forecasting the evolution of hormonal dynamics is a challenging task, but a critical one to improve general understanding of the menstrual cycle and personalized detection of potential health issues. Our goal is to infer and forecast individual hormone daily levels over time, while accommodating pragmatic and minimally invasive measurement settings. To that end, our approach combines the power of probabilistic generative models (i.e., multi-task Gaussian processes) with the flexibility of neural networks (i.e., a dilated convolutional architecture) to learn complex temporal mappings. To attain accurate hormone level reconstruction with as little data as possible, we propose a sampling mechanism for optimal reconstruction accuracy with limited sampling budget. Our results show the validity of our proposed hormonal dynamic modeling framework, as it provides accurate predictive performance across different realistic sampling budgets and outperforms baselines methods.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Knowledge Gaps
Below is a single, consolidated list of concrete knowledge gaps, limitations, and open questions that remain unresolved by the paper. These items are intended to guide actionable future research.
- Lack of external validation on real, longitudinal hormone assays; the framework is only tested on synthetic data, leaving generalization to real-world measurements unproven.
- Limited population scope: the synthetic data are anchored to app users aged 22–30 with natural cycles; applicability to adolescents, perimenopausal women, postpartum periods, diverse ethnicities, and individuals on contraceptives or with conditions (e.g., PCOS, thyroid disorders) is unknown.
- No assessment on anovulatory or atypical cycles; the approach hinges on ovulation timing and LH peaks and may underperform when ovulation is absent or misdetected.
- Synthetic data generation is anchored only on cycle length and ovulation day; potential mismatches in hormone amplitudes, variability, and joint distributions relative to real physiology are not quantified.
- No sensitivity analysis to simulator bias; the impact of mechanistic model mis-specification on learned models and downstream predictions is not evaluated.
- Measurement noise modeling is simplistic (per-hormone i.i.d. Gaussian); real assays have heteroscedastic, non-Gaussian errors and modality differences (serum vs urine vs saliva) that are not accounted for.
- Assumption that all five hormones are sampled simultaneously from serum is impractical for minimally invasive use; the framework does not accommodate partial or asynchronous observations across hormones.
- The non-causal DCNN uses future inputs for reconstruction, which is infeasible for real-time forecasting; causal variants and boundary effects at the sequence edges are not evaluated.
- Uncertainty is not propagated to the final output; the DCNN outputs point estimates without calibrated predictive intervals, hindering risk-aware decision-making.
- Evaluation relies on MSE over standardized units; clinically meaningful endpoints (e.g., ovulation day error, luteal phase length error, peak timing/height error, phase classification accuracy) are not reported.
- Generalization across sampling budgets is untested; it is unclear how models trained under one sampling pattern perform when test-time sampling patterns differ (domain shift).
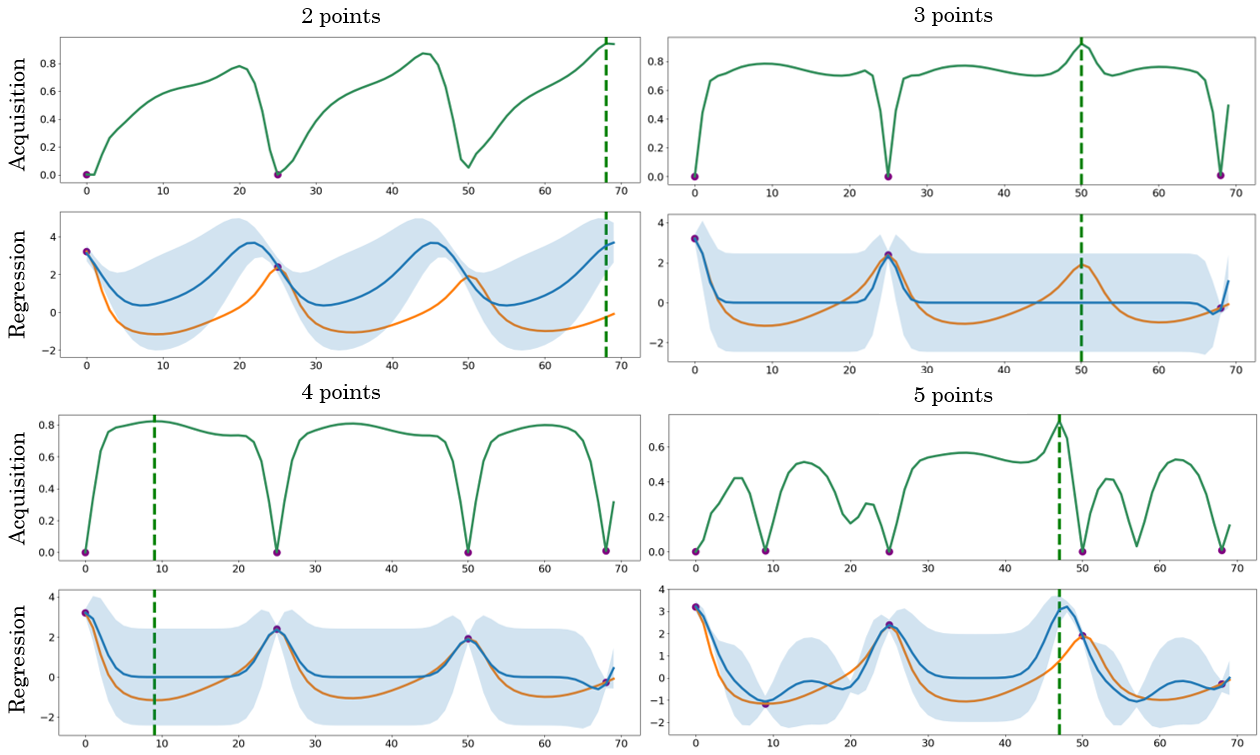
- The Expected Distance (ED) sampling criterion depends on unknown true hormone values y(t), making it infeasible in prospective, real-world data collection; a practical surrogate acquisition (variance-, information-, or ensemble-based) is needed.
- ED sampling is greedy with no analysis of optimality or submodularity; its performance vs alternative acquisition strategies (e.g., UCB, EI, entropy search, A-/D-optimal design) remains unknown.
- Active sampling is performed at the population level; individualized, online/adaptive sampling policies that update as data arrive are not developed.
- Scalability is not addressed; multi-output GP training may become computationally prohibitive for longer horizons, more hormones, or larger cohorts; sparse/structured approximations are not explored.
- The time kernel is stationary and periodic with a single period per individual; it may not capture cycle-to-cycle variability, irregular/anovulatory patterns, or long-term drifts; nonstationary/warped periodic or change-point kernels are not considered.
- The across-hormone kernel assumes linear coregionalization; nonlinear, time-delayed, or phase-shifted inter-hormone relationships are not modeled.
- A priori blockwise grouping (LH/FSH vs E/P/Ih) is assumed rather than learned; data-driven discovery of hormone groups or time-varying dependencies is not explored.
- Robustness to missed or mistimed LH peak measurements is not tested; the setup enforces two LH peaks, which may be unrealistic in practice.
- Baseline comparisons are limited; the LSTM baseline is minimal (single layer with zero imputation), and stronger sequence models (transformers, causal TCNs, state-space models, neural ODEs) are not evaluated.
- Reported training “volatility” is not systematically studied; effects of random seeds, number of MGP samples S, regularization, and optimization hyperparameters lack ablation and reproducibility analysis.
- Interpretability and physiological validation of learned inter-hormone dependencies are not provided; whether learned K(h, h′) aligns with known endocrinology remains unexplored.
- Multimodal signals (BBT, cervical mucus, symptoms, HRV, wearable data) are not incorporated; potential gains from low-cost modalities and their impact on sampling strategy are unknown.
- Missing-not-at-random (MNAR) behavior common in self-tracking is not modeled; assumptions implicitly align with MCAR/MAR.
- Personalization strategy is limited to per-individual MGPs; hierarchical or meta-learning approaches to improve few-shot personalization across users are not investigated.
- Forecast horizon is short (one cycle ahead); performance stability over multiple future cycles and drift over time is not assessed.
- Boundary handling in the non-causal DCNN is unspecified; potential edge artifacts and their impact on reconstruction accuracy are not quantified.
- Fairness and bias analyses are absent; the model’s performance parity across demographic subgroups and health statuses is unknown.
- Practical deployment constraints (adherence, delayed results, cost, clinic schedules) are not modeled; end-to-end evaluation under realistic operational constraints is missing.
- Unit calibration is not discussed; standardized training may mask clinically relevant magnitude errors, and mapping back to assay units with uncertainty is not addressed.
- Hybrid integration with mechanistic ODE models (e.g., data assimilation under sparse observations) is not explored; potential gains in identifiability and interpretability are untested.
- Open-source resources are minimal (60 synthetic individuals); full reproducible pipelines, ED implementations usable without ground truth, learned kernels, and pretrained models are not provided.
Collections
Sign up for free to add this paper to one or more collections.