- The paper introduces a theoretical bound linking true returns to model-based returns while controlling model errors and policy shifts.
- It proposes short, branched rollouts in MBPO to limit compounding bias and achieve significant sample efficiency gains compared to model-free methods.
- Empirical results on continuous control benchmarks validate MBPO’s robust performance and scalability, matching state-of-the-art returns.
Model-Based Policy Optimization: Theoretical Foundations and Empirical Analysis
Introduction
The paper "When to Trust Your Model: Model-Based Policy Optimization" (1906.08253) provides a comprehensive theoretical and empirical investigation into the design of data-efficient and reliable model-based reinforcement learning (MBRL) algorithms. It addresses the practical and theoretical limitations of existing MBRL approaches, particularly the challenge of compounding model errors during long rollouts, and introduces Model-Based Policy Optimization (MBPO). The methodology combines theoretical performance guarantees with pragmatic regularization and control of model usage, yielding significant improvements in sample efficiency and scalability over prevailing model-based and model-free baselines.
Theoretical Analysis of Model-Based RL
The analysis begins by deriving a framework for monotonic improvement in model-based policy optimization. The central performance bound relates the actual return in the true MDP, η[π], to the return under the learned model, η^[π], penalized by a compounding constant C(ϵm,ϵπ) that depends on model generalization error ϵm and the policy distribution shift ϵπ:
η[π]≥η^[π]−[(1−γ)22γmax(ϵm+2ϵπ)+(1−γ)4maxϵπ]
This result formalizes a pessimistic worst-case bound, indicating that unless model error and distribution shift are tightly controlled, improvement in the true environment cannot be guaranteed through optimization in the learned dynamics.
However, empirical insights into model generalization demonstrate that, with sufficient training data, the adverse effects of distribution shift are mitigated. Specifically, as the model training set grows, not only does the generalization error on the training distribution decrease, but sensitivity to policy shifts also diminishes, enabling safer off-policy usage of the model for generating synthetic experience.
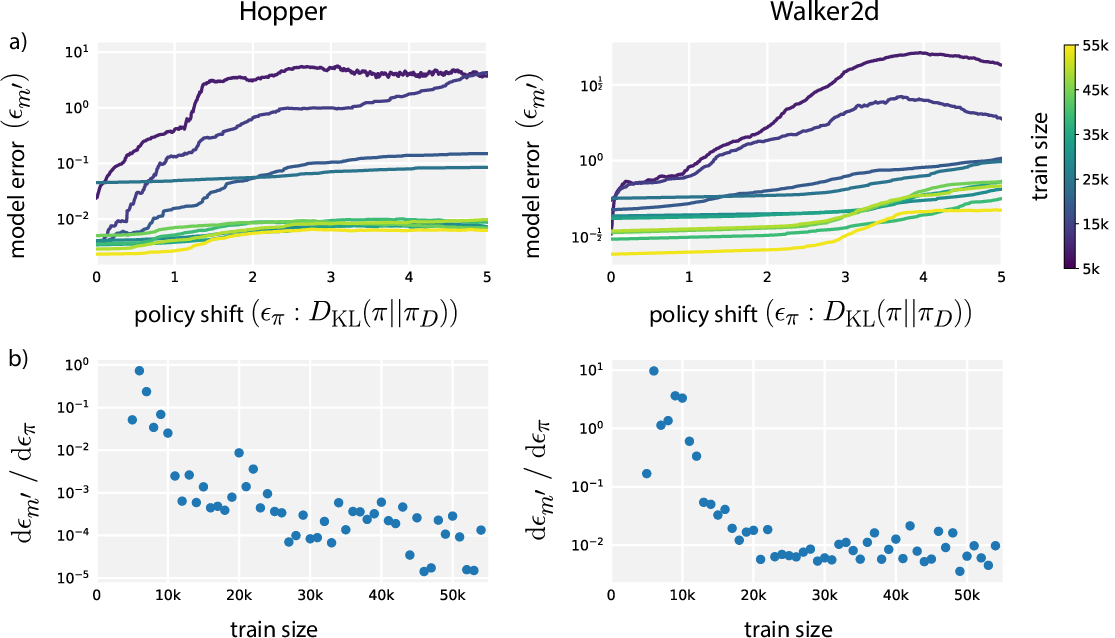
Figure 1: (a) Model generalization error as a function of KL-divergence from the data-collecting policy and quantity of training data; (b) Local sensitivity of model error to policy divergence.
MBPO leverages these insights to interpolate between model-based and model-free approaches, proposing short "branched" rollouts: bootstrapping model predictions from real states rather than simulating from scratch, thus decoupling model rollout length from the task horizon. Theoretical results further refine the usage of empirical model error under policy shift, offering less conservative (tighter) bounds and justifying nonzero-length model rollouts when empirical error is low.
Practical Algorithm Design
MBPO is instantiated with the following components:
- Model Architecture: An ensemble of probabilistic neural networks captures both epistemic and aleatoric uncertainty, with output distributions modeling state transitions and rewards.
- Policy Learner: The algorithm employs Soft Actor-Critic (SAC) for actor-critic optimization, taking advantage of improved data efficiency by using short model-generated rollouts for additional training.
- Model Usage Protocol: Rather than long horizon simulations, MBPO samples short rollouts (typically 1 to 15 steps) initialized from novel states drawn from the replay buffer, thereby preventing the rapid accumulation of model bias and variance.
This design choice is validated empirically, with MBPO achieving high throughput by dramatically increasing the number of model-based updates per real-world interaction without sacrificing asymptotic performance.
Empirical Results
The experimental results are comprehensive. MBPO is compared against SAC, PPO, PETS, STEVE, and SLBO on standard MuJoCo locomotion tasks, using the canonical 1000-step task horizons rather than truncated or simplified settings. Key findings include:
Ablation studies further decompose the role of model rollouts and policy update frequency:
Model exploitation, a major concern in MBRL (where the policy might overfit to exploited errors in the learned model), is empirically analyzed. For sufficiently short rollouts, policy returns under the learned model remain highly correlated with those under the environment, indicating limited model exploitation. Visualizations demonstrate divergence between real and model-based trajectories for long horizons, reinforcing the benefit of the short horizon design.
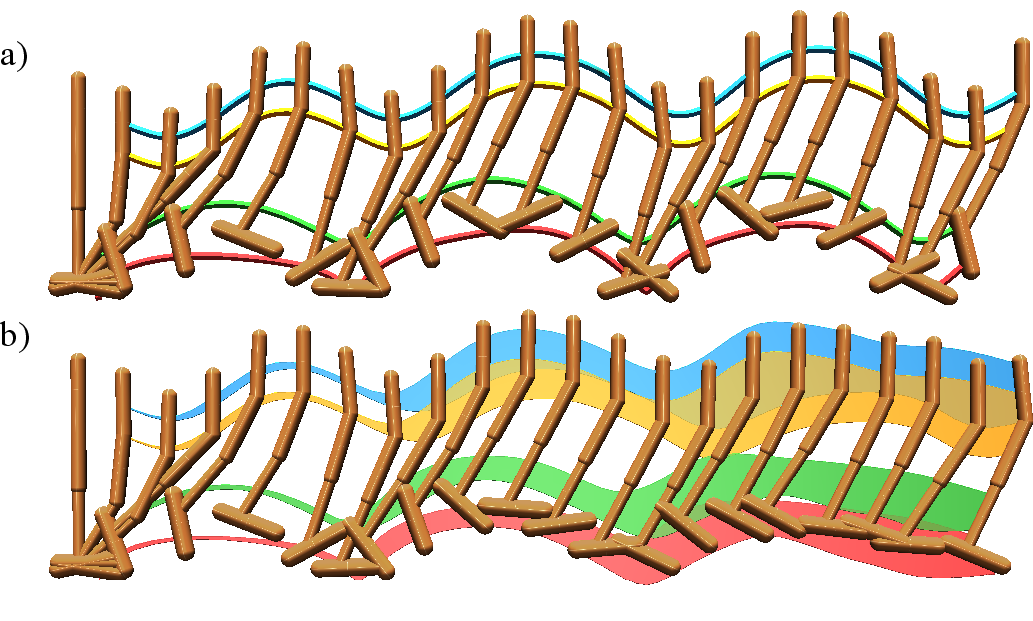

Figure 4: Visualization of real and model-based Hopper rollouts, highlighting the accumulation of predictive uncertainty, and comparison of empirical returns in both settings.
Implications and Future Directions
This work has several profound implications for MBRL:
- Sample Efficiency: MBPO demonstrates that prudent reliance on short, branched rollouts unlocks substantial efficiency gains while safeguarding against model bias.
- Scalability: The method scales to longer-horizon and higher-dimensional tasks without recourse to model-free fine-tuning.
- Algorithmic Justification: The theoretical framework, modified with empirical generalization measurements, provides principled guidelines for model usage and rollout length selection.
Going forward, further developments may focus on adaptive control of rollout lengths based on online error estimation, integration with more complex model architectures for rich observation spaces, and extension to real-world robotic and partially observed domains. The tight coupling between theory and empirical diagnostics in MBPO provides a template for future work in safety-critical or high-stakes RL deployments.
Conclusion
"When to Trust Your Model: Model-Based Policy Optimization" delivers a rigorous approach to model usage in deep RL, balancing data efficiency with robust performance. The theoretical analysis contextualizes the challenge of compounding model error, and the empirical results validate that limited, short-horizon model usage maximizes sample efficiency while achieving state-of-the-art performance across diverse continuous control benchmarks. The MBPO framework represents a significant advance in practical MBRL, and the methodology outlined is likely to influence subsequent approaches to safe and data-efficient reinforcement learning.






