- The paper demonstrates the unavoidable trade-off between natural accuracy and adversarial robustness by decomposing robust error into natural and boundary errors.
- The paper develops tight bounds using classification-calibrated surrogate loss theory to connect surrogate minimization with robust error performance.
- The paper introduces TRADES, a regularized adversarial training method that empirically enhances robustness while controlling standard accuracy loss across benchmark datasets.
Theoretically Principled Trade-off Between Robustness and Accuracy
Introduction
This paper rigorously investigates the adversarial robustness–accuracy trade-off in supervised classification. The authors formalize the gap between natural (standard) and robust classification errors, introduce tight uniform bounds leveraging classification-calibrated loss theory, and propose TRADES, an adversarial defense scheme based on minimizing a novel regularized loss. Strong empirical results are established across benchmark datasets, including a decisive win in the NeurIPS 2018 Adversarial Vision Challenge, outperforming other methods in terms of required perturbation distance for misclassification (1901.08573).
Foundations: Decomposition of Robust Error
The core theoretical insight is the decomposition of robust classification error (Rrob) as the sum of natural error (Rnat) and boundary error (Rbdy):
Rrob(f)=Rnat(f)+Rbdy(f)
This directly relates adversarial vulnerability to the probability mass of inputs near the classifier’s decision boundary. The authors show that the robust error always upper bounds the natural error, with equality when the perturbation radius ϵ=0.
A simple illustrative example demonstrates that the Bayes-optimal classifier can be perfectly accurate but maximally vulnerable to adversarial perturbations; in contrast, a trivial all-one classifier achieves the optimal robust error at the cost of natural accuracy. This underscores that enhancing robustness inevitably incurs loss in standard accuracy.

Figure 1: Counterexample illustrating the accuracy-robustness trade-off, where increasing robustness requires a suboptimal natural error.
Tight Bounds via Classification-Calibrated Surrogate Loss
Since direct minimization of the robust 0–1 error is intractable, the authors tightly relate surrogate loss minimization to robust error. Leveraging the theory of classification-calibrated losses, they derive an upper bound:
Rrob(f)−Rnat∗≤ψ−1(Rϕ(f)−Rϕ∗)+E[x′∈B(x,ϵ)maxϕ(f(x′)f(x)/λ)]
where ψ is a function that connects excess surrogate risk to excess 0–1 risk. A matching lower bound is obtained, showing the upper bound is tight for common losses (hinge, logistic, exponential). These results establish the statistical limits of adversarial training with surrogate losses and clarify the inevitability of the robustness–accuracy tension.


Figure 2: Comparison of boundary neighborhoods for linear and nonlinear classifiers, visualizing how more complex boundaries increase adversarial vulnerability.
TRADES: Trade-off-Inspired Regularization
Inspired by the above decomposition, the TRADES defense is introduced. TRADES minimizes:
E[ϕ(f(x),y)]+λ1E[x′∈B(x,ϵ)maxϕ(f(x),f(x′))]
The first term optimizes for standard accuracy, while the second term explicitly penalizes predictions that lack smoothness with respect to adversarial perturbations. The hyperparameter λ provides direct control over the accuracy-robustness trade-off. For multi-class settings, the framework is generalized by adopting a multiclass-calibrated loss (e.g., cross-entropy).
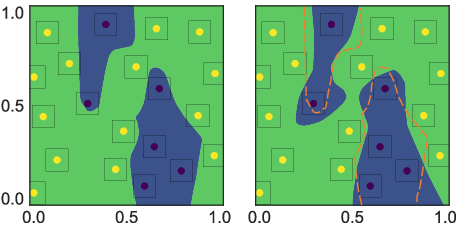
Figure 3: Comparison of decision boundaries learned by natural training and adversarial training, showing TRADES pushes the boundary away from data mass, thereby reducing robust error.
Experimental Results
Extensive evaluations were performed on MNIST, CIFAR-10, and Tiny ImageNet, testing both white-box and black-box threat models using various attack techniques, such as FGSM, PGD, DeepFool, and boundary attacks.
The impact of λ is systematically studied, verifying the theoretical prediction: as regularization is strengthened (lower λ), robust accuracy increases at the cost of standard accuracy. TRADES is empirically robust not only to white-box attacks but also to transfer-based (black-box) attacks and unrestricted attacks involving spatial transformations.




Figure 5: Visualization of adversarial examples on MNIST highlighting imperceptible perturbations that fool typical models; TRADES-trained models maintain correct predictions.




Figure 6: Adversarial examples for CIFAR10 generated via FGSMk, displaying the effectiveness of robust training in resisting adversarial perturbations.
Theoretical and Practical Implications
Theoretically, this work formalizes the fundamental trade-off in adversarial learning. Any effort to increase robustness via conventional surrogate loss minimization is proven to necessarily reduce standard accuracy for all distributions. The role of boundary error clarifies why deep (nonlinear) models, with complex decision surfaces, are typically more vulnerable than linear classifiers for the same data distribution.
Practically, TRADES demonstrates how regularized adversarial training can be scaled to large models and datasets. The method’s scalability and empirical superiority set a new baseline for robust deep learning. The optimization is amenable to stochastic gradient methods, and subsequent research leverages acceleration schemes to mitigate computational costs.






Figure 7: Adversarial examples (boundary attack with spatial transformation) on a TRADES-trained ResNet-50; adversarial images become clearly of the alternative class, yet the classifier remains robust.






Figure 8: On ‘bird’ examples, adversarial perturbations become clearly ‘bicycle’-like, again showing successful defense by TRADES-trained models.
Future Directions
The methodology motivates further exploration in several directions:
- Integrating TRADES with architectural modifications (e.g., Parseval networks, feature denoising) for improved robustness.
- Developing efficient large-scale optimization algorithms for adversarial training.
- Investigating the sample complexity gap induced by adversarial regularization and further bridging theoretical insights and practical defense design.
- Extending TRADES to unrestricted and more general threat models, including distributional and functional robustness perspectives.
Conclusion
This paper rigorously identifies and quantifies the inescapable trade-off between robustness and accuracy in classification. The introduction of TRADES provides a theoretically guided, scalable, and empirically validated framework for balancing this trade-off, establishing new standards for adversarial defense. Its results have both clarified limitations inherent in robust learning and underpinned the design of state-of-the-art adversarially robust models.
(1901.08573)
























