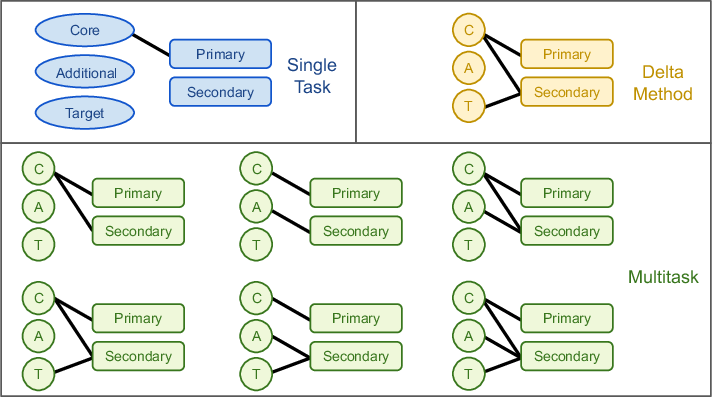
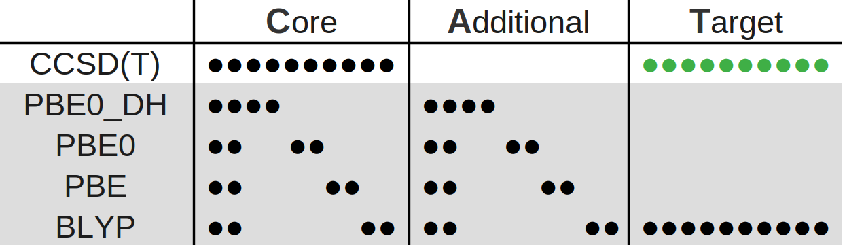
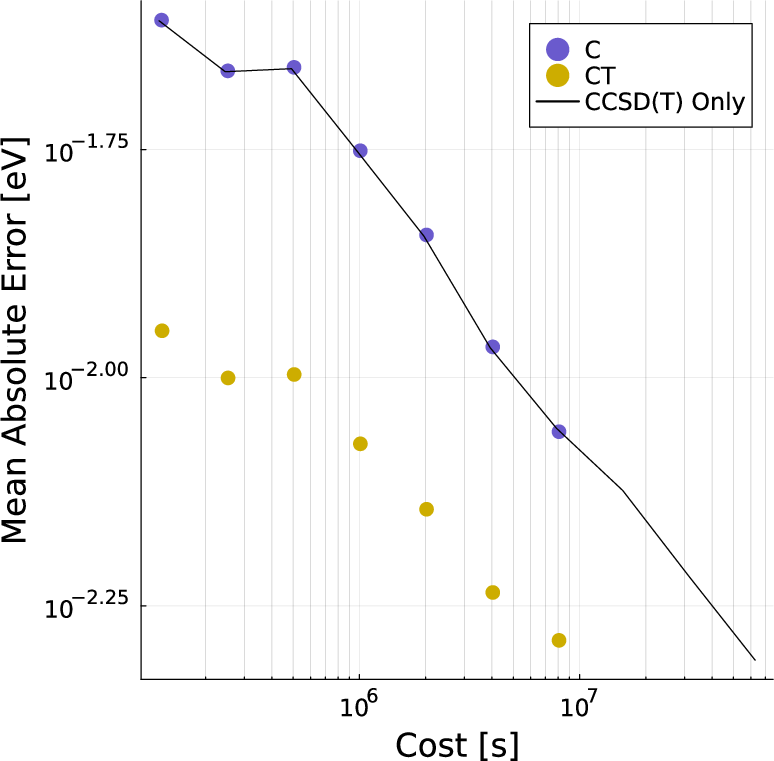
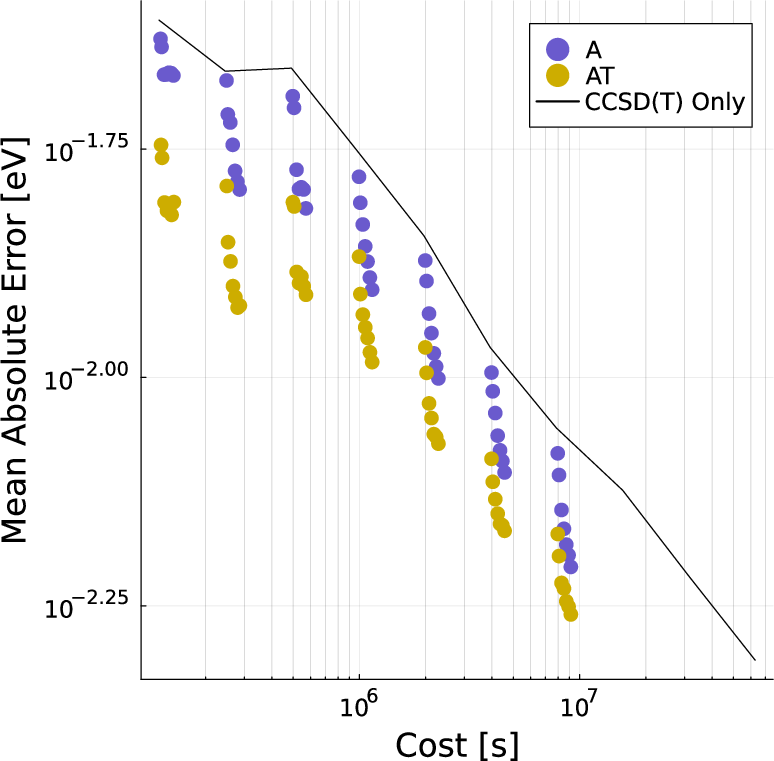
Multitask methods for predicting molecular properties from heterogeneous data (2401.17898v2)

Abstract: Data generation remains a bottleneck in training surrogate models to predict molecular properties. We demonstrate that multitask Gaussian process regression overcomes this limitation by leveraging both expensive and cheap data sources. In particular, we consider training sets constructed from coupled-cluster (CC) and density functional theory (DFT) data. We report that multitask surrogates can predict at CC-level accuracy with a reduction to data generation cost by over an order of magnitude. Of note, our approach allows the training set to include DFT data generated by a heterogeneous mix of exchange-correlation functionals without imposing any artificial hierarchy on functional accuracy. More generally, the multitask framework can accommodate a wider range of training set structures -- including full disparity between the different levels of fidelity -- than existing kernel approaches based on $\Delta$-learning, though we show that the accuracy of the two approaches can be similar. Consequently, multitask regression can be a tool for reducing data generation costs even further by opportunistically exploiting existing data sources.

• The paper introduces a multitask Gaussian process regression framework that integrates heterogeneous data sources to predict molecular properties.
• Experiments on water trimers and organic molecules show improved performance compared to single-task and Δ-learning models using flexible training sets.
• The study highlights cost reduction and enhanced accuracy by efficiently combining high-fidelity and low-fidelity data in computational material science.

Multitask Methods for Predicting Molecular Properties from Heterogeneous Data

Introduction to Multitask Gaussian Process Regression

Predicting molecular properties accurately remains a challenge due to the scaling complexities of quantum-mechanical calculations, such as the Schrödinger equation. Multitask Gaussian process regression (GPR) offers a pathway to leverage multiple data sources, combining high-cost, high-fidelity data (like coupled-cluster computations) with more affordable, lower fidelity data (such as density functional theory calculations). This approach enables prediction accuracy akin to the high-cost method while significantly lowering data generation costs. It achieves this by using a framework that can incorporate heterogeneous data from various sources without imposing a hierarchy on the functional accuracy, overcoming limitations of traditional kernel-based methods like $\Delta$-learning.

Figure 1: Diagram of training data sets compatible with the considered methods. The Core, Additional, and Target systems are related to the primary method (CCSD(T)) and various secondary methods.

Statistical Models and Methods

Gaussian Process Regression

GPR models predict the value of a quantity, $f(\bm{X})$, using noisy observations $\bm{Y}_i = f(\bm{X}_i) + \varepsilon_i$. This involves selecting a mean function $\mu(\bm{X})$ and a kernel function $k(\cdot, \cdot)$, which define the covariance matrix used for inference. The result is a posterior distribution allowing prediction of target values conditioned on observations.

Multifidelity and Multitask Modeling

The multifidelity approach models relationships between high and low fidelity data using scaling parameters and disparity functions, while multitask modeling considers multiple Gaussian process tasks with shared and specific components related through a primary function. Multitask regression facilitates flexible data integration, useful for datasets from heterogeneous methods, as shown in Fig. 1.

Experimental Setup for Multitask Regression

Data Generation

Two case studies illustrate the approach: predicting three-body interaction energies in water trimers and ionization potential for small organic molecules. For water trimers, secondary data was generated using DFT with PBE and SCAN functionals, whereas for organic molecules, ionization potential was calculated using various functionals including PBE0, PBE0_DH, and BLYP.

Performance Metrics and Flexible Training Sets

Multitask modeling performs better than single task regression models across different training set configurations. Training sets are structured to include different combinations of Core (C), Additional (A), and Target (T) data, with varying overlap between secondary tasks.

Figure 2: Example data set structures. Different molecule configurations are used for various training tasks.

Key Advantages and Experimental Results

Multitask Flexibility and Results

An experiment comparing multitask models to single task models demonstrated consistent improvement, especially when secondary data overlaps with target predictions. Tests show benefits in incorporating multiple secondary tasks, with a focus on efficiency and flexibility in training set design.

Figure 3: Correlation between different methods of global feature construction.

Comparison to $\Delta$-learning

Multitask methods outperform $\Delta$-learning when modeling and predicting differences between quantum chemical methods. The flexibility of multitask framework allows the use of multiple datasets without an arbitrary order, enhancing model performance.

Conclusion

Multitask GPR provides a robust framework for integrating heterogeneous data, reducing costs and enhancing prediction accuracy for molecular properties. The flexibility in training sets and the correlation-based integration of secondary tasks make it a valuable tool in computational material science, with potential for further exploration in neural networks and transfer learning contexts. Future work could optimize correlation parameters to refine the multitask $\Delta$ option further, ensuring that it always outperforms traditional $\Delta$ models.